WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

DihedralGroup
✖
DihedralGroup

✖

represents the dihedral group of order 2n.

Details

  • The degree n of DihedralGroup[n] must be a positive integer.
  • DihedralGroup[1] is isomorphic to CyclicGroup[2] and represented by default as a permutation group on the points {1,2}.
  • DihedralGroup[2] is isomorphic to AbelianGroup[{2,2}] and represented by default as a permutation group on the points {1,2,3,4}.
  • For n≥3, DihedralGroup[n] is represented by default as a permutation group on the points {1,…,n}.

Background & Context

  • DihedralGroup[n] represents the dihedral group 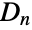of order 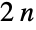(also denoted 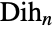or 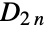) for a given positive integer n. For 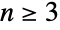, the default representation of DihedralGroup[n] is as a permutation group on the symbols . The special cases DihedralGroup[1] and DihedralGroup[2] are isomorphic to CyclicGroup[2] and AbelianGroup[{2,2}], respectively, and are represented by default as a permutation group on the symbols 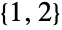and 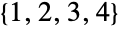, respectively.
  • Mathematically, the dihedral group 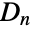consists of the 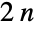symmetries of a regular 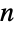-gon, namely its 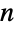rotational symmetries and 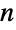reflection symmetries. In particular, 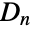consists of elements 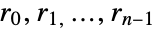(rotations) and 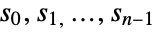(reflections), which combine to transform under its group operation according to the identities 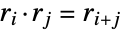, , 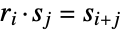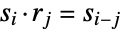and 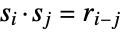, where addition and subtraction are performed modulo 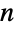. 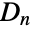is a permutation group, but for 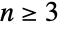, the operations of reflection and rotation fail to commute in general, meaning 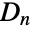is nonabelian for .
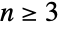  • Dihedral groups are important in the analysis of regular structures, including in the determination of properties for symmetric chemical compounds and in crystallography.
  • The usual group theoretic functions may be applied to DiherdalGroup[n], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the dihedral group 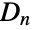are available via FiniteGroupData[{"DihedralGroup",n},"prop"].
  • DihedralGroup is related to a number of other symbols. DihedralGroup[n] is isomorphic to the semidirect product of CyclicGroup[n] and CyclicGroup[2] (with the latter acting on the former by inversion), and for 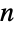even, DihedralGroup[n] is isomorphic to the direct product of DihedralGroup[n/2] and CyclicGroup[2]. For 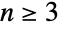, the dihedral group 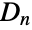is a subgroup of the symmetric group 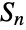. Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AbelianGroup, AlternatingGroup, CyclicGroup and SymmetricGroup.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Number of elements of a dihedral group:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-5qbh14
Out[1]=1

Permutation generators of a dihedral group:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-11euhb
Out[1]=1

Elements of a permutation representation of a dihedral group:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-eshlmr
Out[1]=1

Scope  (1)Survey of the scope of standard use cases

DihedralGroup[n] for any positive integer n:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-qfdt6b

Properties & Relations  (1)Properties of the function, and connections to other functions

DihedralGroup[1] and DihedralGroup[2] are the only dihedral commutative groups:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-iyrpbm
In[2]:=2
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-33odit

Possible Issues  (1)Common pitfalls and unexpected behavior

DihedralGroup[1] and DihedralGroup[2] are special as permutation groups because they are not subgroups of SymmetricGroup[1] and SymmetricGroup[2], respectively. Their permutation representations require larger supports:

In[1]:=1
✖
https://wolfram.com/xid/08uxlv9kjsxmrci-wwy5p6
Out[1]=1
Wolfram Research (2010), DihedralGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralGroup.html.
✖
Wolfram Research (2010), DihedralGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralGroup.html.

Text

Wolfram Research (2010), DihedralGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralGroup.html.

✖
Wolfram Research (2010), DihedralGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralGroup.html.

CMS

Wolfram Language. 2010. "DihedralGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DihedralGroup.html.

✖
Wolfram Language. 2010. "DihedralGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DihedralGroup.html.

APA

Wolfram Language. (2010). DihedralGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DihedralGroup.html

✖
Wolfram Language. (2010). DihedralGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DihedralGroup.html

BibTeX

@misc{reference.wolfram_2025_dihedralgroup, author="Wolfram Research", title="{DihedralGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DihedralGroup.html}", note=[Accessed: 07-June-2025 ]}

✖
@misc{reference.wolfram_2025_dihedralgroup, author="Wolfram Research", title="{DihedralGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DihedralGroup.html}", note=[Accessed: 07-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_dihedralgroup, organization={Wolfram Research}, title={DihedralGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/DihedralGroup.html}, note=[Accessed: 07-June-2025 ]}

✖
@online{reference.wolfram_2025_dihedralgroup, organization={Wolfram Research}, title={DihedralGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/DihedralGroup.html}, note=[Accessed: 07-June-2025 ]}