AbelianGroup[{n1,n2,…}]
表示次数为 n1,n2,… 的循环群的直积.


AbelianGroup
AbelianGroup[{n1,n2,…}]
表示次数为 n1,n2,… 的循环群的直积.
背景
- AbelianGroup[{n1,n2,…,nk}] 表示交换群,其定义为非负整数次 n1,n2,…,nk 循环群的直接乘积
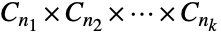 . 这里,群
. 这里,群 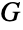 、
、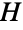 、… 的直接乘积是底层集合为有序元组
、… 的直接乘积是底层集合为有序元组 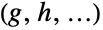 的集合的笛卡尔乘积模拟,其中
的集合的笛卡尔乘积模拟,其中 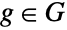 ,
, 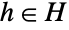 , … 且群运算是逐个分量进行,有
, … 且群运算是逐个分量进行,有 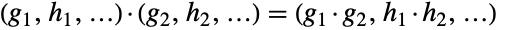 .
. - 一般来说,术语“阿贝尔群”用于表示一个可交换的群,即对于所有元素
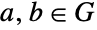 ,群
,群 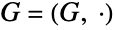 ,群运算
,群运算  满足等式
满足等式 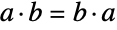 . 有限阿贝尔群的基本定理表明,每个有限的阿贝尔群都可以表示为循环群的直接乘积. 因此,函数 AbelianGroup 可以用于表示任何有限的阿贝尔群.
. 有限阿贝尔群的基本定理表明,每个有限的阿贝尔群都可以表示为循环群的直接乘积. 因此,函数 AbelianGroup 可以用于表示任何有限的阿贝尔群. - AbelianGroup[{n1,n2,…,nk}] 的默认表示为元素
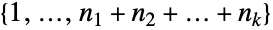 的置换群. 当
的置换群. 当 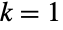 时,AbelianGroup[{n}] 等价于 CyclicGroup[n](其中 AbelianGroup[{0}] 和 AbelianGroup[{1}] 相当于恰好有一个元素的平凡群).
时,AbelianGroup[{n}] 等价于 CyclicGroup[n](其中 AbelianGroup[{0}] 和 AbelianGroup[{1}] 相当于恰好有一个元素的平凡群). - 通常的群理论函数可以应用于 AbelianGroup[{n1,n2,…,nk}],包括 GroupOrder、GroupGenerators、GroupElements 等等. 阿贝尔群 AbelianGroup[{n1,n2,…,nk}] 的一些预计算属性通过 FiniteGroupData[{"AbelianGroup",{n1,n2,…,nk}},"prop"] 可用.
- AbelianGroup 与许多其它符号相关. 数学上,AbelianGroup[{n1,n2,…,nk}] 等价于群 CyclicGroup[n1],CyclicGroup[n2],…,CyclicGroup[nk] 的直接乘积. 通过整数参数化的 Wolfram 语言内置有限群的其它无限族包括 AlternatingGroup、CyclicGroup、DihedralGroup 和 SymmetricGroup.
范例
打开所有单元 关闭所有单元属性和关系 (2)
对于非零的次数,AbelianGroup[{n1,n2,…}] 的阶数是 ni 的乘积:
一个 p 为素数群 AbelianGroup[{p,p,…}] 称为基本阿贝尔群. 在这种群中,所有非平凡元素的阶数都是 p:
相关链接
文本
Wolfram Research (2010),AbelianGroup,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AbelianGroup.html.
CMS
Wolfram 语言. 2010. "AbelianGroup." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AbelianGroup.html.
APA
Wolfram 语言. (2010). AbelianGroup. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AbelianGroup.html 年
BibTeX
@misc{reference.wolfram_2025_abeliangroup, author="Wolfram Research", title="{AbelianGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AbelianGroup.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_abeliangroup, organization={Wolfram Research}, title={AbelianGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/AbelianGroup.html}, note=[Accessed: 05-February-2026]}