AlternatingGroup
次数 n の交代群である.
詳細
- AlternatingGroup[n]の次数 n は,非負の整数でなければならない.次数0,1,2は,自明群あるいは恒等群に対応する.
- AlternatingGroup[n]はデフォルトで点{1,…,n}の置換群として表される.
予備知識
- AlternatingGroup[n]は,与えられた非負の整数 n について n 個の記号の交代群
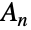 (
(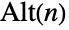 と書かれることもある)を表す.
と書かれることもある)を表す.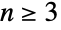 のとき,AlternatingGroup[n]のデフォルト表現は記号
のとき,AlternatingGroup[n]のデフォルト表現は記号 についての置換群としてである.特殊なケースであるAlternatingGroup[0],AlternatingGroup[1],AlternatingGroup[2]は厳密に1つの元を持つ自明群に等しい.
についての置換群としてである.特殊なケースであるAlternatingGroup[0],AlternatingGroup[1],AlternatingGroup[2]は厳密に1つの元を持つ自明群に等しい. - 数学的には,
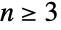 の交代群
の交代群 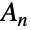 は記号
は記号 の
の 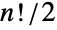 回の偶置換(つまり,交代記号が
回の偶置換(つまり,交代記号が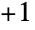 である
である の置換)と合成の群操作からなる.交代群は,したがって,次数
の置換)と合成の群操作からなる.交代群は,したがって,次数 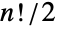 の置換群である.AlternatingGroup[n]はPermutationGroup[perms]と同型である.ただし,perms=Select[Permutations[Range[n]],Signature[#]1&]である.
の置換群である.AlternatingGroup[n]はPermutationGroup[perms]と同型である.ただし,perms=Select[Permutations[Range[n]],Signature[#]1&]である. - 交代群は,抽象代数学,幾何学的群論,表現論,組合せ論,数理物理学において根本的な重要性を持つ.数多くの重要な数学的結果が交代群について成り立つ.例えば,
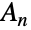 のすべての元が3の巡回(長さが3に等しい置換)として書けることに注目することで,
のすべての元が3の巡回(長さが3に等しい置換)として書けることに注目することで,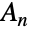 は
は 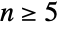 について単純(つまり,自明ではない正規部分群を持たない)なことになる.この事実は有限単純群の分類に重要な役割を果たす.これに加え,(n が小さい)交代群とリー(Lie)型のある種の小さい群の間には数多くの例外同型が存在する.最後に,交代群のホモロジー群は n が大きくなるにつれて一定になると意味で安定していることが知られている.
について単純(つまり,自明ではない正規部分群を持たない)なことになる.この事実は有限単純群の分類に重要な役割を果たす.これに加え,(n が小さい)交代群とリー(Lie)型のある種の小さい群の間には数多くの例外同型が存在する.最後に,交代群のホモロジー群は n が大きくなるにつれて一定になると意味で安定していることが知られている. - AlternatingGroup[n]には,GroupOrder,GroupGenerators,GroupElements等を含む通常の群論関数を適用することができる.
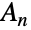 の数多くの計算済み特性をFiniteGroupData[{"AlternatingGroup",n},"prop"]によって得ることができる.
の数多くの計算済み特性をFiniteGroupData[{"AlternatingGroup",n},"prop"]によって得ることができる. - AlternatingGroupは数多くの他のシンボルと関連している.交代群と二面体群はどちらも対称群の重要な部分群である.Wolfram言語に組み込まれた,整数でパラメータ化される他の有限群の無限族には,AbelianGroup,CyclicGroup,DihedralGroup,SymmetricGroupがある.
テキスト
Wolfram Research (2010), AlternatingGroup, Wolfram言語関数, https://reference.wolfram.com/language/ref/AlternatingGroup.html.
CMS
Wolfram Language. 2010. "AlternatingGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AlternatingGroup.html.
APA
Wolfram Language. (2010). AlternatingGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AlternatingGroup.html
BibTeX
@misc{reference.wolfram_2025_alternatinggroup, author="Wolfram Research", title="{AlternatingGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AlternatingGroup.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_alternatinggroup, organization={Wolfram Research}, title={AlternatingGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/AlternatingGroup.html}, note=[Accessed: 10-March-2026]}

