AlternatingGroup
表示次数为 n 的交错群.
更多信息
- AlternatingGroup[n] 的次数 n 必须是一个非负整数. 次数 0、1 和 2 对应于平凡群或者单位群.
- 默认情况下，AlternatingGroup[n] 表示为点 {1,…,n} 上的一个置换群.
背景
- AlternatingGroup[n] 表示 n 个符号上的交错群
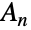（有时表示为
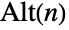），其中 n 为已知的非负整数. 当 
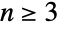时，AlternatingGroup[n] 的默认表示为符号 
上的置换群. 特殊情况 AlternatingGroup[0]、AlternatingGroup[1] 和 AlternatingGroup[2] 等价于恰好有1个元素的平凡群. - 数学上，交错群
（
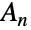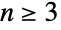）由符号 
的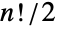 
个偶数置换组成（即 
的置换符号为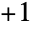 
的那些置换），连同组合的群运算. 因此交错群是阶为 
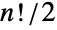的置换群，其中 AlternatingGroup[n] 与 PermutationGroup[perms] 同构，其中 perms=Select[Permutations[Range[n]],Signature[#]1&]. - 交错群在抽象代数、几何群论、表示论、组合论和数学物理学中至关重要. 很多重要的数学结果适用于交错群. 例如，通过注意到
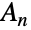的每个元素可以写作3个轮换的组合（长度等于3的置换），从而有 
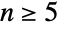时，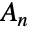
是简单的（即没有非平凡正态子群），这在有限简单群的分类中发挥了关键作用. 此外，在交错群（对于 n 小）和某些 Lie 类型的小群之间存在许多异常同构. 最后，就随着 n 增大而变得恒定的意义上而言，已知交错群的群同源性是稳定的. - 通常的群理论函数可以应用于 AlternatingGroup[n]，包括 GroupOrder、GroupGenerators、GroupElements 等等. 交错群
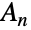的一些预计算属性通过 FiniteGroupData[{"AlternatingGroup",n},"prop"] 可用. - AlternatingGroup 与许多其它符号相关. 交错群和二面体群都是对称群的重要子群. 通过整数参数化的 Wolfram 语言内置有限群的其它无限族包括 AbelianGroup、CyclicGroup、DihedralGroup 和 SymmetricGroup.
范例
打开所有单元关闭所有单元
Wolfram Research (2010)，AlternatingGroup，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingGroup.html.
文本
Wolfram Research (2010)，AlternatingGroup，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingGroup.html.
CMS
Wolfram 语言. 2010. "AlternatingGroup." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AlternatingGroup.html.
APA
Wolfram 语言. (2010). AlternatingGroup. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AlternatingGroup.html 年