AngleBisector
AngleBisector[{q1,p,q2}]
gives the bisector of the interior angle at p formed by the triangle with vertex points p, q1 and q2.
AngleBisector[{q1,p,q2},"type"]
gives the angle bisector of the specified type.
Details
- AngleBisector gives an InfiniteLine object.
- The qi and p in AngleBisector[{q1,p,q2}] can be lists of coordinates or explicit Point objects.
- AngleBisector[p{q1,q2}] is equivalent to AngleBisector[{q1,p,q2}].
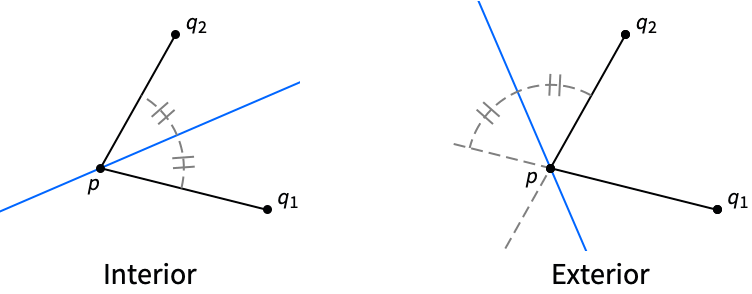
- AngleBisector gives the line that divides the angle into two equal angles and that passes through the point p.
- The following bisector type specifications "type" can be given:
-
"Interior" bisector of the interior angle of the triangle at p "Exterior" bisector of the exterior angle of the triangle at p - AngleBisector only works in 2D.
- AngleBisector can be used with symbolic points in GeometricScene.
Examples
open all close allProperties & Relations (4)
AngleBisector finds the interior angle bisector by default:
The angle bisector divides the angle into two equal angles:
The exterior angle bisector divides the exterior angle into two equal angles:
TriangleConstruct[{a,b,c},"AngleBisector"] is equivalent to AngleBisector[{a,b,c}]:
Possible Issues (2)
Text
Wolfram Research (2019), AngleBisector, Wolfram Language function, https://reference.wolfram.com/language/ref/AngleBisector.html.
CMS
Wolfram Language. 2019. "AngleBisector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AngleBisector.html.
APA
Wolfram Language. (2019). AngleBisector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AngleBisector.html