TriangleConstruct[tri,type]
gives the specified type of construct for the triangle tri.




TriangleConstruct
TriangleConstruct[tri,type]
gives the specified type of construct for the triangle tri.
Details





- TriangleConstruct can give a Point, Line, InfiniteLine, Circle or Triangle object.
- The triangle tri can be given as {p1,p2,p3}, Triangle[{p1,p2,p3}] or Polygon[{p1,p2,p3}].
- The following point types can be given:
-
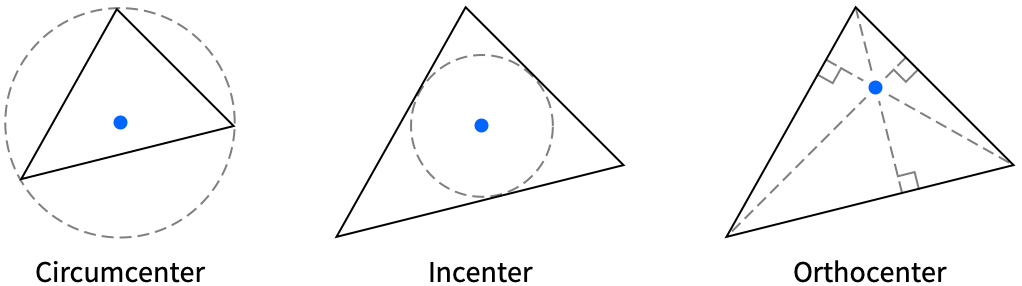
{"AngleBisectingCevianEndpoint",p} endpoint of the cevian bisecting the angle at the vertex p "Centroid" centroid {"CevianEndpoint",center,p} endpoint of the cevian passing through the vertex p and the specified center "Circumcenter" center of the circumcircle {"Excenter",p} center of the excircle opposite from the vertex p {"Foot",p} foot of the altitude passing through the vertex p "Incenter" center of the incircle {"Midpoint",p} midpoint of the side opposite from the vertex p "NinePointCenter" center of nine-point circle "Orthocenter" orthocenter {"SymmedianEndpoint",p} endpoint of the symmedian passing through the vertex p "SymmedianPoint" symmedian point - The following line types can be given:
-
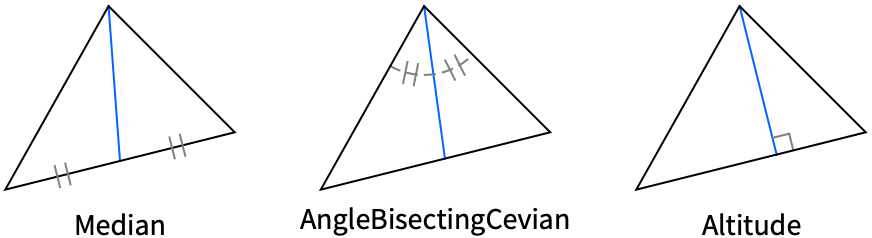
{"Altitude",p} altitude passing through the vertex p {"AngleBisectingCevian",p} cevian bisecting the interior angle at the vertex p {"AngleBisector",p} bisector of the interior angle at the vertex p "Boundary" boundary {"Cevian",center,p} cevian passing through the vertex p and the specified center "EulerLine" Euler line {"ExteriorAngleBisector",p} bisector of the exterior angle at the vertex p {"Median",p} median passing through the vertex p {"OppositeSide",p} side opposite from the vertex p {"PerpendicularBisector",p} perpendicular bisector of the side opposite from p {"Symmedian",p} symmedian passing through the vertex p - The following circle types can be given:
-
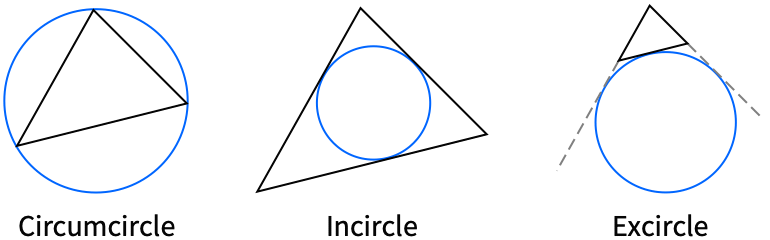
"Circumcircle" circumscribed circle {"Excircle",p} excircle opposite from the vertex p "Incircle" inscribed circle "NinePointCircle" nine-point circle - The following triangle types can be given:
-
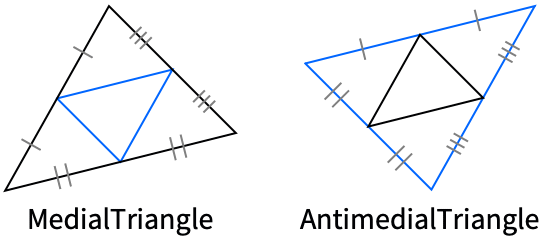
"AntimedialTriangle" antimedial triangle "MedialTriangle" medial triangle "Triangle" original triangle - In the form {"type",p}, p can be a symbolic point specification in a GeometricScene, or it can be an explicit vertex of the form {x,y}, Point[{x,y}] or the index i of the vertex. When given in the short form "type", the vertex p2 is used.
- In the forms {"CevianEndpoint",center,p} and {"Cevian",center,p}, the center can be given as a center type such as "Centroid" or as a point specification. When given in the short form {"CevianEndpoint",center}, the vertex p2 is used.
- In any form that specifies a vertex p, a value of All will return a list of three values corresponding to the vertices.
- TriangleConstruct can be used with symbolic points in GeometricScene.
Examples
open all close allBasic Examples (2)
Scope (29)
Points (12)
Calculate the endpoint of an angle bisector:
Calculate the centroid of a triangle:
Calculate the endpoint of a cevian passing through the orthocenter:
Calculate the endpoint of a cevian passing through a different vertex:
Calculate the endpoint of a cevian through an arbitrary center point:
Calculate the circumcenter of a triangle:
Calculate the excenter of a triangle at the specified vertex:
Calculate all of the excenters:
Calculate the foot of an altitude of a triangle at the specified vertex:
Calculate the incenter of a triangle:
Calculate the midpoint of a side of a triangle:
Calculate the nine-point center of a triangle:
Calculate the orthocenter of a triangle:
Lines (10)
Calculate the altitude of a triangle:
Calculate the angle bisector of a triangle:
Get the angle bisector as a line segment:
Calculate the boundary of a triangle:
Calculate a cevian passing through the orthocenter:
Calculate the cevian passing through a different vertex:
Calculate a cevian through an arbitrary center point:
Calculate the Euler line of a triangle:
Calculate the exterior angle bisector at a vertex:
Calculate a median of a triangle:
Calculate the side opposite from a specified vertex:
Calculate the perpendicular bisector of a side of a triangle:
Circles (4)
Properties & Relations (28)
Angle Bisector and Incenter (5)
An angle bisector endpoint is the intersection of an angle bisector and the opposite side:
The angle bisectors of a triangle intersect at the incenter:
TriangleConstruct[{a,b,c},"AngleBisector"] is equivalent to AngleBisector[{a,b,c}]:
TriangleConstruct[{a,b,c},"Incircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Incenter"],TriangleMeasurement[{a,b,c},"Inradius"]]:
TriangleConstruct[{a,b,c},"Incircle"] is equivalent to Circle@@Insphere[{a,b,c}]:
Median, Midpoint and Centroid (3)
A median intersects the opposite side at the midpoint:
The medians of a triangle intersect at the centroid:
TriangleConstruct[{a,b,c},"Centroid"] is equivalent to Point[RegionCentroid[Triangle[{a,b,c}]]]:
Perpendicular Bisector, Midpoint and Circumcenter (5)
The perpendicular bisector of a side passes through the midpoint of that side:
The perpendicular bisectors of a triangle intersect at the circumcenter:
TriangleConstruct[{a,b,c},"PerpendicularBisector"] is equivalent to PerpendicularBisector[{a,c}]:
TriangleConstruct[{a,b,c},"Circumcircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Circumcenter"],TriangleMeasurement[{a,b,c},"Circumradius"]]:
TriangleConstruct[{a,b,c},"Circumcircle"] is equivalent to Circle@@Circumsphere[{a,b,c}]:
Altitude, Foot and Orthocenter (2)
Symmedian, Median and Angle Bisector (3)
Exterior Angle Bisector and Excenter (3)
The excenter opposite from a vertex is the intersection of the exterior angle bisectors of the opposite angles:
TriangleConstruct[{a,b,c},"ExteriorAngleBisector"] is equivalent to AngleBisector[{a,b,c},"Exterior"]:
TriangleConstruct[{a,b,c},"Excircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Excenter"],TriangleMeasurement[{a,b,c},"Exradius"]]:
Nine-Point Circle, Foot, Midpoint, Orthocenter (2)
The nine-point circle of a triangle passes through the feet of the altitudes, the midpoints of the sides and the midpoints of the segments from the vertices to the orthocenter:
TriangleConstruct[{a,b,c},"NinePointCircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"NinePointCenter"],TriangleMeasurement[{a,b,c},"NinePointRadius"]]:
Euler Line, Centroid, Circumcenter, Orthocenter and Nine-Point Center (1)
Midpoint (1)
TriangleConstruct[{a,b,c},"Midpoint"] is equivalent to Point[Midpoint[{a,c}]]:
Boundary (1)
TriangleConstruct[{a,b,c},"Boundary"] is equivalent to RegionBoundary[Triangle[{a,b,c}]]:
Medial and Antimedial Triangle (2)
TriangleConstruct[{a,b,c},"MedialTriangle"] is equivalent to Triangle[TriangleCenter[tri,{"Midpoint",All}]]:
The antimedial triangle is the triangle whose medial triangle is the original triangle:
Related Guides
History
Text
Wolfram Research (2019), TriangleConstruct, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangleConstruct.html.
CMS
Wolfram Language. 2019. "TriangleConstruct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TriangleConstruct.html.
APA
Wolfram Language. (2019). TriangleConstruct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangleConstruct.html
BibTeX
@misc{reference.wolfram_2025_triangleconstruct, author="Wolfram Research", title="{TriangleConstruct}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/TriangleConstruct.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_triangleconstruct, organization={Wolfram Research}, title={TriangleConstruct}, year={2019}, url={https://reference.wolfram.com/language/ref/TriangleConstruct.html}, note=[Accessed: 03-March-2026]}