AppellF1[a,b1,b2,c,x,y]
二変数のアッペル(Appell)超幾何関数 ![]() である.
である.


AppellF1
AppellF1[a,b1,b2,c,x,y]
二変数のアッペル(Appell)超幾何関数 ![]() である.
である.
詳細

- AppellF1は,超幾何級数を一般化して多項式係数を持つHorn偏微分方程式系を解Appell関数族の一員である.
- 記号操作・数値操作の両方に適した数学関数である.
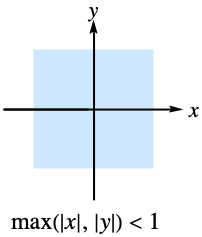
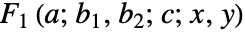 は,領域
は,領域![max(TemplateBox[{x}, Abs],TemplateBox[{y}, Abs])<1 max(TemplateBox[{x}, Abs],TemplateBox[{y}, Abs])<1](Files/AppellF1.ja/3.png) の中で収束する超幾何級数
の中で収束する超幾何級数 ![sum_(m=0)^inftysum_(n=0)^infty(TemplateBox[{a, {m, +, n}}, Pochhammer] TemplateBox[{{b, _, 1}, m}, Pochhammer] TemplateBox[{{b, _, 2}, n}, Pochhammer] )/(TemplateBox[{c, {m, +, n}}, Pochhammer]m! n!)x^m y^n sum_(m=0)^inftysum_(n=0)^infty(TemplateBox[{a, {m, +, n}}, Pochhammer] TemplateBox[{{b, _, 1}, m}, Pochhammer] TemplateBox[{{b, _, 2}, n}, Pochhammer] )/(TemplateBox[{c, {m, +, n}}, Pochhammer]m! n!)x^m y^n](Files/AppellF1.ja/4.png) を介して主定義を得る.
を介して主定義を得る.- 引数の実数値についてのアッペルF1級数の収束領域は以下の通りである.
- 一般に,
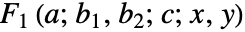 は
は 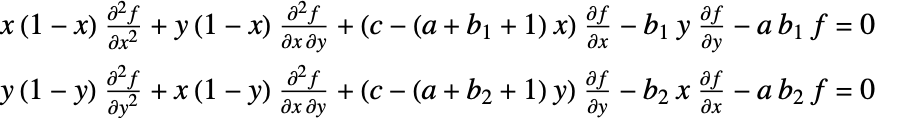 の形のHorn偏微分方程式系を満足する. »
の形のHorn偏微分方程式系を満足する. » 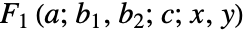 は
は 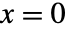 または
または 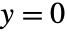 のとき,
のとき,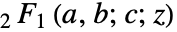 に簡約される.
に簡約される.- 特別な引数の場合,AppellF1は自動的に厳密値を計算する.
- AppellF1は任意の数値精度で評価できる.
- AppellF1[a,b1,b2,c,x,y]は,二変数
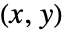 複素空間で
複素空間で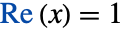 および
および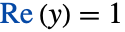 を満たす特異線を有し,
を満たす特異線を有し,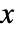 および
および 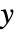 で
で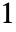 から
から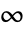 に伸びる半直線に沿って不連続な分枝切断線を有する.
に伸びる半直線に沿って不連続な分枝切断線を有する. - FullSimplifyおよびFunctionExpandはAppellF1の変換規則を含んでいる.
例題
すべて開く すべて閉じる例 (8)
Infinityにおける級数展開:
スコープ (28)
数値評価 (6)
特定の値 (4)
可視化 (4)
関数の特性 (9)
級数展開 (2)
特性と関係 (2)
おもしろい例題 (1)
初等関数および特殊関数の多くはAppellF1の特殊ケースである:
テクニカルノート
-
▪
- 特殊関数
履歴
1999 で導入 (4.0) | 2023 で更新 (13.3)
テキスト
Wolfram Research (1999), AppellF1, Wolfram言語関数, https://reference.wolfram.com/language/ref/AppellF1.html (2023年に更新).
CMS
Wolfram Language. 1999. "AppellF1." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/AppellF1.html.
APA
Wolfram Language. (1999). AppellF1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AppellF1.html
BibTeX
@misc{reference.wolfram_2025_appellf1, author="Wolfram Research", title="{AppellF1}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/AppellF1.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_appellf1, organization={Wolfram Research}, title={AppellF1}, year={2023}, url={https://reference.wolfram.com/language/ref/AppellF1.html}, note=[Accessed: 10-March-2026]}