ArrayMesh[array]
generates a mesh region from an array of rank d in which each cell has a geometric dimension d and represents a nonzero value of the array.




ArrayMesh
ArrayMesh[array]
generates a mesh region from an array of rank d in which each cell has a geometric dimension d and represents a nonzero value of the array.
Details and Options
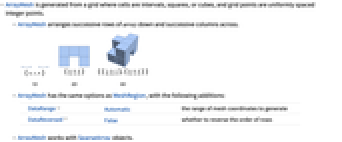
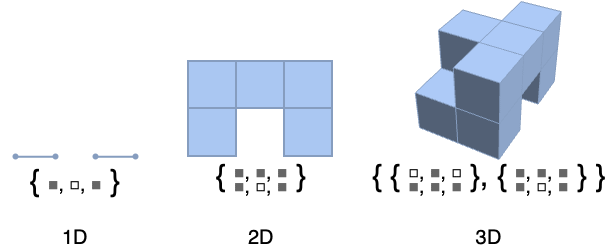
- ArrayMesh is generated from a grid where cells are intervals, squares, or cubes, and grid points are uniformly spaced integer points.
- ArrayMesh arranges successive rows of array down and successive columns across.
- ArrayMesh has the same options as MeshRegion, with the following additions:
-
DataRange Automatic the range of mesh coordinates to generate DataReversed False whether to reverse the order of rows - ArrayMesh works with SparseArray objects.
Examples
open all close allScope (2)
Options (14)
DataRange (1)
DataRange allows you to specify the range of mesh coordinates to generate:
DataReversed (1)
DataReversed allows you to reverse the order of rows:
MeshCellHighlight (2)
MeshCellHighlight allows you to specify highlighting for parts of an ArrayMesh:
MeshCellLabel (2)
MeshCellLabel can be used to label parts of an ArrayMesh:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of an ArrayMesh:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction can be used to assign values to parts of an ArrayMesh:
MeshCellStyle (3)
MeshCellStyle allows you to specify styling for parts of an ArrayMesh:
Individual cells can be highlighted using their cell index:
Give explicit color directives to specify colors for individual cells:
Applications (15)
Cellular Automaton (5)
Image (2)
Convert a 2D image to a MeshRegion:
Pattern (2)
SubstitutionSystem (4)
Properties & Relations (6)
The output of ArrayMesh is always a full-dimensional MeshRegion:
ArrayMesh consists of intervals in 1D:
ArrayPlot can be used to generate a plot:
MatrixPlot can be used to generate a plot:
Find a boundary mesh region by using BoundaryMesh:
DataRange-> range is equivalent to using RescalingTransform[{...}, range]:
Use RescalingTransform:
Related Guides
History
Text
Wolfram Research (2016), ArrayMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayMesh.html.
CMS
Wolfram Language. 2016. "ArrayMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayMesh.html.
APA
Wolfram Language. (2016). ArrayMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayMesh.html
BibTeX
@misc{reference.wolfram_2025_arraymesh, author="Wolfram Research", title="{ArrayMesh}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayMesh.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arraymesh, organization={Wolfram Research}, title={ArrayMesh}, year={2016}, url={https://reference.wolfram.com/language/ref/ArrayMesh.html}, note=[Accessed: 17-February-2026]}