AugmentedSymmetricPolynomial

AugmentedSymmetricPolynomial[{r1,r2,…}]

represents a formal augmented symmetric polynomial with exponents r1, r2, ….

AugmentedSymmetricPolynomial[{{r11,…,r1n},{r21,…,r2n},…}]

represents a multivariate formal augmented symmetric polynomial with exponent vectors {r11, …, r1n}, {r21, …, r2n}, ….

AugmentedSymmetricPolynomial[rspec,data]

gives the augmented symmetric polynomial in data.

Details

  • AugmentedSymmetricPolynomial[{r1,…,rk},{x1,…,xn}] is given by 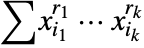, where the sum is taken over the index set 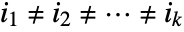and .
  • In the multivariate case, ri and xi are vectors and xiri is interpreted as xi1ri1xi2ri2⋯.
  • AugmentedSymmetricPolynomial[rspec] can be used to represent formal augmented symmetric sums used in moment estimators.
  • MomentConvert can be used to generate moment estimators in terms of AugmentedSymmetricPolynomial objects.
  • MomentEvaluate can be used to evaluate polynomials of formal AugmentedSymmetricPolynomial objects on a dataset.

Examples

open allclose all

Basic Examples  (1)

Scope  (2)

Use MomentEvaluate to evaluate formal augmented symmetric polynomials on data:

TraditionalForm formatting:

Applications  (1)

Linearize polynomials in AugmentedSymmetricPolynomial:

Properties & Relations  (1)

AugmentedSymmetricPolynomial with a single exponent is equivalent to PowerSymmetricPolynomial:

This relationship also holds for the multivariate generalization:

Wolfram Research (2010), AugmentedSymmetricPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html.

Text

Wolfram Research (2010), AugmentedSymmetricPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html.

CMS

Wolfram Language. 2010. "AugmentedSymmetricPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html.

APA

Wolfram Language. (2010). AugmentedSymmetricPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html

BibTeX

@misc{reference.wolfram_2024_augmentedsymmetricpolynomial, author="Wolfram Research", title="{AugmentedSymmetricPolynomial}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html}", note=[Accessed: 26-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_augmentedsymmetricpolynomial, organization={Wolfram Research}, title={AugmentedSymmetricPolynomial}, year={2010}, url={https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html}, note=[Accessed: 26-April-2024 ]}