AutocorrelationTest

AutocorrelationTest[data]

tests whether the data is autocorrelated.

AutocorrelationTest[data,k]

tests whether the data is autocorrelated up to lag k.

AutocorrelationTest[data,k,"property"]

returns the value of "property" for a given model.

Details and Options

  • AutocorrelationTest performs a hypothesis test for randomness on data with the null hypothesis 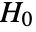that the autocorrelations ρ1=ρ2=…=ρk==0 and alternative 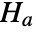that at least one of the ρi≠0.
  • Rejecting the null hypothesis allows the conclusion that the data is not random.
  • By default, a probability value or 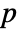-value is returned.
  • A small 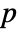-value suggests that randomness is unlikely.
  • The data can be a list of values {x1,x2,…,xn} or a TemporalData object.
  • The lag k can be Automatic or a positive integer such that k<n.
  • If k is not given, it is taken to be Automatic.
  • Setting k to Automatic gives k=Ceiling[Log[n]]].
  • AutocorrelationTest[data,k,"test"] reports the 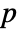-value according to "test".
  • The following tests can be used for univariate data with all paths of equal length n:
  • "LjungBox"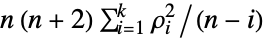
    "BoxPierce"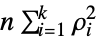
  • For multivariate data:
  • "LjungBox"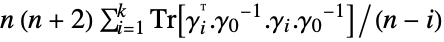
    "BoxPierce"n sum_(i=1)^kTr[TemplateBox[{{(, {gamma, _, i}, )}}, Transpose].TemplateBox[{{(, {gamma, _, 0}, )}}, Inverse].gamma_i.TemplateBox[{{(, {gamma, _, 0}, )}}, Inverse]]
  • AutocorrelationTest[data,k,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • AutocorrelationTest[data,k,"property"] can be used to directly give the value of "property".
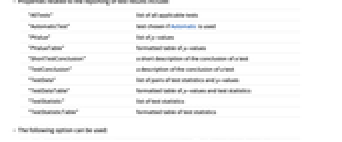
  • Properties related to the reporting of test results include:
  • "AllTests"list of all applicable tests
    "AutomaticTest"test chosen if Automatic is used
    "PValue"list of 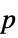-values
    "PValueTable"formatted table of 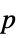-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 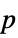-values
    "TestDataTable"formatted table of 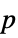-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • The following option can be used:
  • SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For unit root tests, a cutoff 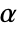is chosen such that 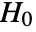is rejected only if 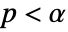. The value of 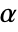used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 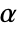is set to 0.05.

Examples

open allclose all

Basic Examples  (1)

Test whether data is random:

The data is autocorrelated:

Scope  (14)

Testing  (10)

Test time-series data for autocorrelation:

The -values are typically large when the data is not autocorrelated:

The -values are typically small when the data is autocorrelated:

Test vector data:

Test for autocorrelation up to lag 5:

Setting the lag to Automatic is equivalent to using Ceiling[Log[n]]:

Perform a particular test for autocorrelation:

Any number of tests can be performed simultaneously:

Using Automatic applies the Ljung–Box test:

The property "AutomaticTest" can be used to show which test is used:

Perform all tests appropriate to the data simultaneously:

Use the property "AllTests" to identify which tests were used:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from the HypothesisTestData object:

The -value and test statistic from the "LjungBox" test:

Extract any number of properties simultaneously:

The -value and test statistic from a Box–Pierce test:

Reporting  (4)

Tabulate the results from a selection of tests:

A full table of all appropriate test results:

A table of selected test results:

Retrieve the entries from a test table for customized reporting:

The -values are above 0.05, so there is not enough evidence to reject at that level:

Tabulate -values for a test or group of tests:

The -value from the table:

A table of -values from all appropriate tests:

A table of -values from a subset of tests:

Report the test statistic from a test or group of tests:

The test statistic from the table:

A table of test statistics from all appropriate tests:

Options  (1)

SignificanceLevel  (1)

The significance level is used for "TestConclusion" and "ShortTestConclusion":

Applications  (2)

An instructor asked her students to generate a sequence of 100 random bits with the software of their choice. She warned that she would recognize bits that were not generated appropriately. The following data shows two such examples. One student used a random number generator as asked and the other scribbled down some bits just before class. Find which student is which:

It appears that the second student did not do the assignment correctly:

Fit a time-series model to some monthly average temperature data for Chicago over a 10-year period. An adequate model should have uncorrelated residuals:

The data is highly autocorrelated:

The model residuals are uncorrelated, suggesting an adequate model was selected:

Possible Issues  (1)

Only the first path of TemporalData is tested:

Compare to testing only the first path:

Wolfram Research (2014), AutocorrelationTest, Wolfram Language function, https://reference.wolfram.com/language/ref/AutocorrelationTest.html.

Text

Wolfram Research (2014), AutocorrelationTest, Wolfram Language function, https://reference.wolfram.com/language/ref/AutocorrelationTest.html.

CMS

Wolfram Language. 2014. "AutocorrelationTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AutocorrelationTest.html.

APA

Wolfram Language. (2014). AutocorrelationTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AutocorrelationTest.html

BibTeX

@misc{reference.wolfram_2024_autocorrelationtest, author="Wolfram Research", title="{AutocorrelationTest}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AutocorrelationTest.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_autocorrelationtest, organization={Wolfram Research}, title={AutocorrelationTest}, year={2014}, url={https://reference.wolfram.com/language/ref/AutocorrelationTest.html}, note=[Accessed: 18-November-2024 ]}