BilateralLaplaceTransform
BilateralLaplaceTransform[expr,t,s]
expr の両側ラプラス(Laplace)変換を与える.
BilateralLaplaceTransform[expr,{t1,t2,…,tn},{s1,s2,…,sn}]
expr の多次元両側ラプラス変換を与える.
詳細とオプション

- 関数
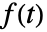 の両側ラプラス変換は
の両側ラプラス変換は 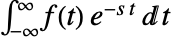 と定義される.
と定義される. - 多次元両側ラプラス変換は
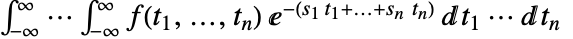 で与えられる.
で与えられる. - 第3引数 s が数値で与えられているなら積分は数値法を使って計算される.
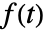 の両側ラプラス変換は
の両側ラプラス変換は 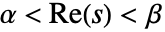 であるような
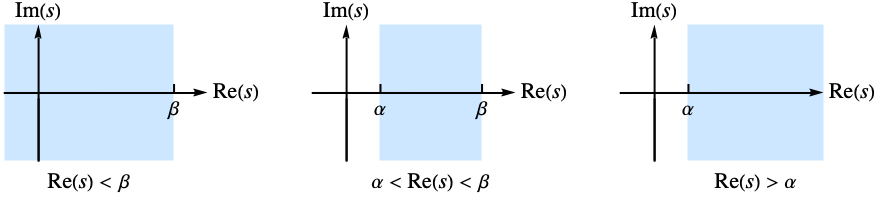
であるような 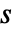 の複素数値についてのみ存在する.場合によってはこの定義が半平面まで及ぶことがある.
の複素数値についてのみ存在する.場合によってはこの定義が半平面まで及ぶことがある.- 次は,使用可能なオプションである.
-
AccuracyGoal Automatic 目標とする絶対確度の桁数 Assumptions $Assumptions パラメータについての仮定 GenerateConditions True パラメータについての条件を含む答を生成するかどうか Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal 最適化しようとするパフォーマンスの局面 PrecisionGoal Automatic 目標とする精度の桁数 PrincipalValue False コーシー(Cauchy)主値を求めるかどうか WorkingPrecision Automatic 内部計算精度
例題
すべて開くすべて閉じる例 (2)
スコープ (20)
一変量関数 (8)
数値評価 (2)
形式的特性 (8)
BilateralLaplaceTransformは線形演算子である:
オプション (4)
Assumptions (1)
Assumptionsを使ってパラメータの範囲を指定する:
GenerateConditions (1)
GenerateConditionsをFalseに設定して条件なしの結果を得る:
PrincipalValue (1)
以下の関数の両側変換は ![]() における特異点のために定義されない:
における特異点のために定義されない:
PrincipalValueを使って積分のコーシー主値を得る:
WorkingPrecision (1)
WorkingPrecisionを使って結果を任意精度で得る:
特性と関係 (2)
BilateralLaplaceTransformとInverseBilateralLaplaceTransformは互いに互いの逆関数である:
NIntegrateを使って数値近似を得る:
NIntegrateは両側ラプラスパラメータ s の数値について変換を計算する:
テキスト
Wolfram Research (2021), BilateralLaplaceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.
CMS
Wolfram Language. 2021. "BilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.
APA
Wolfram Language. (2021). BilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html