WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

InverseBilateralLaplaceTransform
✖
InverseBilateralLaplaceTransform

✖

gives the inverse bilateral Laplace transform of expr.

✖
InverseBilateralLaplaceTransform[expr,{s1,s2,…,sn},{t1,t2,…,tn}]

gives the multidimensional inverse bilateral Laplace transform of expr.

Details and Options

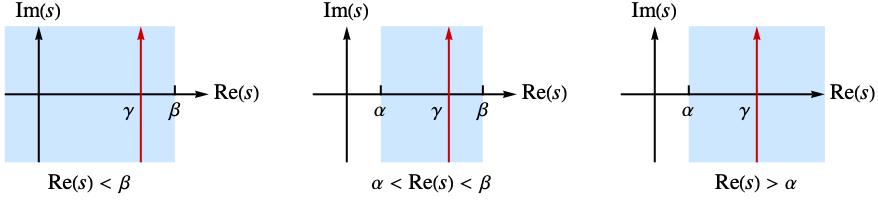
  • The inverse bilateral Laplace transform of a function 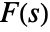is defined to be 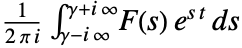, where the integration is along a vertical line 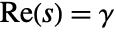, lying in a strip 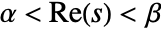in which the function 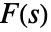is holomorphic. In some cases, the strip of analyticity may extend to a half-plane.
  • The multidimensional inverse bilateral Laplace transform of a function 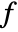is given by a contour integral of the form .
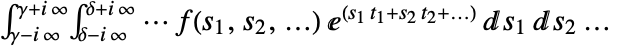  • The integral is computed using numerical methods if the third argument, 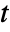, is given a numerical value.
  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditionsFalsewhether to generate answers that involve conditions on parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    WorkingPrecisionAutomaticthe precision used in internal computations

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Inverse bilateral Laplace transform of a function:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-g7y74o
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-usbmnw

Function with a parameter:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-34mymg

Plot the result:

In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-858h6c

Scope  (13)Survey of the scope of standard use cases

Inverse bilateral Laplace transform of rational function with two real poles:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-yuu6wa

Rational function with two real and two complex poles:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-3j6aov

The following function has two real and four complex poles:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-y525zg
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-4dys4g
In[3]:=3
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-1mdbcd
In[4]:=4
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-7xbzal

Inverse bilateral Laplace transform of a product of rational and exponential functions:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-6i01lu

A rational function with different strips of convergences has different inverse bilateral Laplace transforms:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-505trt
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-lh8c5r
In[3]:=3
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-2f8cp3
In[4]:=4
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-te24k8

Rational function whose region of convergence is in the left half-plane:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-74thmm

Function with region of convergence in the right half-plane:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-lrtzg6
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-ufywdx

The inverse bilateral Laplace transform of the following rational function is a decaying sinusoidal wave:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-8d94wx
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-rrf50t

Inverse bilateral Laplace transform of a function that is analytic in the whole complex plane:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-gwc85p
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-vozysp

Inverse bilateral Laplace transform leading to a Gaussian function:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-pqqn3o

Inverse bilateral Laplace transform of a constant is a Dirac delta function:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-rx21du

Evaluate the inverse bilateral Laplace transform at a single point:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-kin0zu

Inverse bilateral Laplace transform at a single point for an analytic function:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-tu4oar

Options  (3)Common values & functionality for each option

Assumptions  (3)

Specify the range for a parameter using Assumptions:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-xvve2t

Use Assumptions to place a pole outside the strip of convergence:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-neri75

Use Assumptions to restrict the right end of the convergence strip in the left half-plane:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-jhlsjj

Properties & Relations  (1)Properties of the function, and connections to other functions

InverseBilateralLaplaceTransform and BilateralLaplaceTransform are mutual inverses:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-si5uys
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-f185p5

Neat Examples  (1)Surprising or curious use cases

Create a table of basic inverse bilateral Laplace transforms:

In[1]:=1
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-dsm058
In[2]:=2
✖
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-xl2lur
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.
✖
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.

Text

Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.

✖
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.

CMS

Wolfram Language. 2021. "InverseBilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.

✖
Wolfram Language. 2021. "InverseBilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.

APA

Wolfram Language. (2021). InverseBilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html

✖
Wolfram Language. (2021). InverseBilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html

BibTeX

@misc{reference.wolfram_2025_inversebilaterallaplacetransform, author="Wolfram Research", title="{InverseBilateralLaplaceTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}", note=[Accessed: 27-March-2025 ]}

✖
@misc{reference.wolfram_2025_inversebilaterallaplacetransform, author="Wolfram Research", title="{InverseBilateralLaplaceTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}", note=[Accessed: 27-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inversebilaterallaplacetransform, organization={Wolfram Research}, title={InverseBilateralLaplaceTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}, note=[Accessed: 27-March-2025 ]}

✖
@online{reference.wolfram_2025_inversebilaterallaplacetransform, organization={Wolfram Research}, title={InverseBilateralLaplaceTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}, note=[Accessed: 27-March-2025 ]}