BilateralLaplaceTransform
BilateralLaplaceTransform[expr,t,s]
给出 expr 的双侧拉普拉斯变换.
BilateralLaplaceTransform[expr,{t1,t2,…,tn},{s1,s2,…,sn}]
给出 expr 的多维度双侧拉普拉斯变换.
更多信息和选项

- 函数
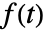 的双侧拉普拉斯变换定义为
的双侧拉普拉斯变换定义为 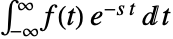 .
. - 多维度双侧拉普拉斯变换由
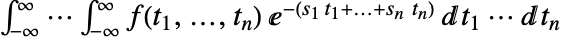 给出.
给出. - 如果第三个参数。s,以数字值给定,则积分由数字方法计算出.
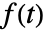 的双侧拉普拉斯变换仅为使得
的双侧拉普拉斯变换仅为使得 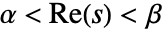 的复值
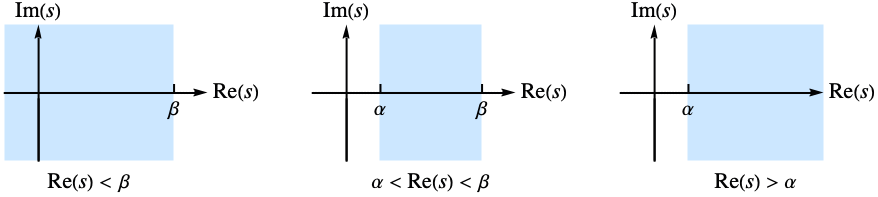
的复值 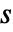 存在. 在某些情况下,这条定义可以扩展到半平面中.
存在. 在某些情况下,这条定义可以扩展到半平面中.- 可以给出如下选项:
-
AccuracyGoal Automatic 绝对精度查询的位数 Assumptions $Assumptions 关于参数要做的假设 GenerateConditions True 是否生成包含参数条件的答案 Method Automatic 要使用的方法 PerformanceGoal $PerformanceGoal 要最优化的性能方面 PrecisionGoal Automatic 精度查询的位数 PrincipalValue False 是否计算柯西主值 WorkingPrecision Automatic 内部计算中使用的精度
范例
打开所有单元关闭所有单元范围 (20)
单变量函数 (8)
数值计算 (2)
形式属性 (8)
BilateralLaplaceTransform 是线性操作符:
选项 (4)
Assumptions (1)
使用 Assumptions 指定参数值域:
GenerateConditions (1)
将 GenerateConditions 设置为 False 可获取没有条件的结果:
PrincipalValue (1)
使用 PrincipalValue 可获取积分的柯西主值:
WorkingPrecision (1)
使用 WorkingPrecision 可获取任意精度的结果:
属性和关系 (2)
BilateralLaplaceTransform 和 InverseBilateralLaplaceTransform 互为反函数:
使用 NIntegrate 可获取近似数值:
NIntegrate 计算双侧拉普拉斯参数 s 的数值:
文本
Wolfram Research (2021),BilateralLaplaceTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.
CMS
Wolfram 语言. 2021. "BilateralLaplaceTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html.
APA
Wolfram 语言. (2021). BilateralLaplaceTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BilateralLaplaceTransform.html 年