WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

CDFWavelet
✖
CDFWavelet

✖

タイプ"9/7"のCohen–Daubechies–Feauveauウェーブレットを表す．

✖
CDFWavelet["type"]

タイプ"type"のCohen–Daubechies–Feauveauウェーブレットを表す．

詳細

  • CDFWaveletは双直交ウェーブレット群を定義する．
  • 使用可能な"type"の形
  • "5/3"JPEG2000の可逆圧縮で使われる
    "9/7"JPEG2000の非可逆圧縮で使われる
  • スケーリング関数(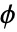)とウェーブレット関数(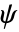)はコンパクトサポートを持つ．両関数は対称である．
  • CDFWaveletはDiscreteWaveletTransform，WaveletPhi等の関数で使うことができる．

例題

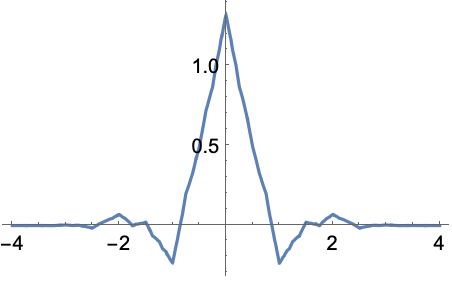
すべて開くすべて閉じる

例  (3)基本的な使用例

スケーリング関数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-gpi6tg
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-gb8f9b
Out[2]=2

ウェーブレット関数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-vc7o0g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-xdbxfp
Out[2]=2

フィルタ係数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-kjry2h
Out[1]=1

スコープ  (16)標準的な使用例のスコープの概要

基本的な用法  (10)

主ローパスフィルタ係数を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-5q3vbl
Out[1]=1

双対ローパスフィルタ係数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-8wgk6z
Out[1]=1

主ハイパスフィルタ係数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-ghmu0m
Out[1]=1

双対ハイパスフィルタ係数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-5utoqa
Out[1]=1

リフティングフィルタ係数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-u5x0a9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-1x7frz
Out[2]=2

関数を生成してリフティングウェーブレット変換を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-nfjqzn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-ol7ejo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-7bq5gu
Out[3]=3

主スケーリング関数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-1hi2ld
Out[1]=1

双対スケーリング関数：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-cpb7tk
Out[2]=2

異なる再帰レベルを使ってスケーリング関数をプロットする：

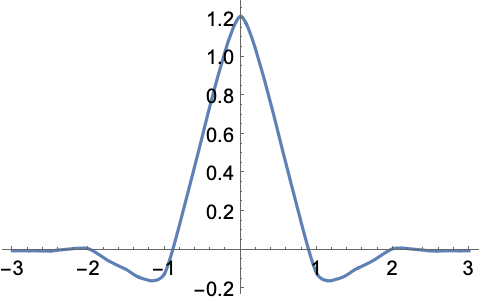
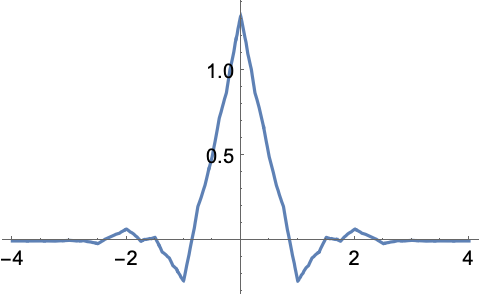
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-jvaues
Out[1]=1

主ウェーブレット関数：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-4fzw6t
Out[1]=1

双対ウェーブレット関数：

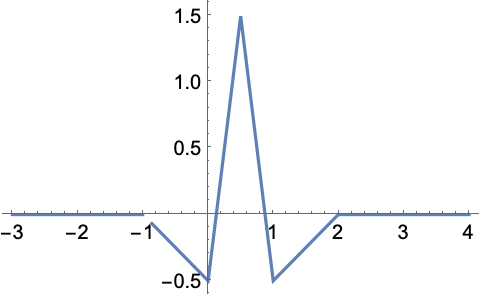
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-pq6kvv
Out[2]=2

異なる再帰レベルを使ってウェーブレット関数をプロットする：

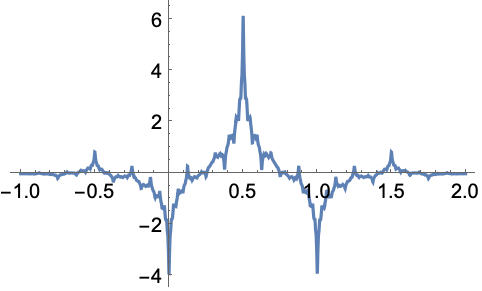
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-b0lb5q
Out[1]=1

ウェーブレット変換  (5)

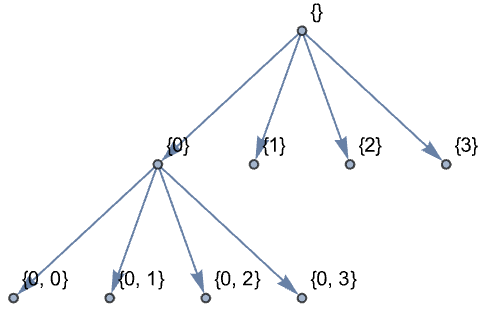
DiscreteWaveletTransformを計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-xhbmxi
Out[1]=1

ウェーブレット係数の木を見る：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-gtqy6c
Out[2]=2

ウェーブレット係数の次元を得る：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-mrjnjd
Out[3]=3

ウェーブレット係数をプロットする：

In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-qx915m
Out[4]=4

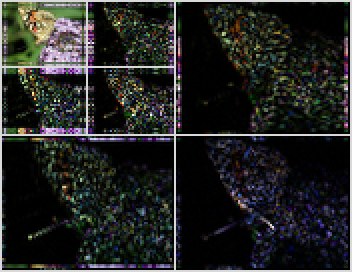
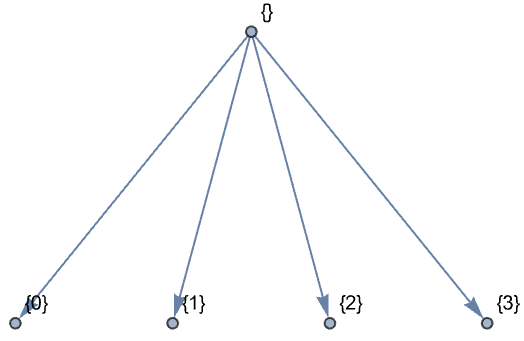
DiscreteWaveletPacketTransformを計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-vtrxi2
Out[1]=1

ウェーブレット係数の木を見る：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-j3n0f1
Out[2]=2

ウェーブレット係数の次元を得る：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-wuwmcl
Out[3]=3

ウェーブレット係数をプロットする：

In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-x0l386
Out[4]=4

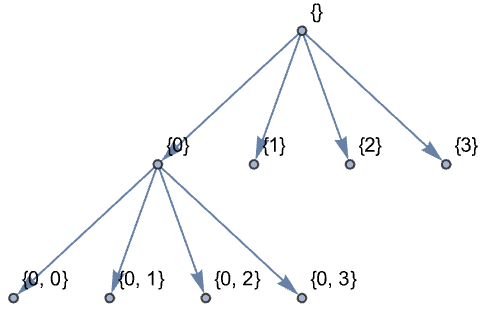
StationaryWaveletTransformを計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-lgbd1m

ウェーブレット係数の木を見る：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-jbb9sz
Out[2]=2

ウェーブレット係数の次元を得る：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-msff83
Out[3]=3

ウェーブレット係数をプロットする：

In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-kn3y3t
Out[4]=4

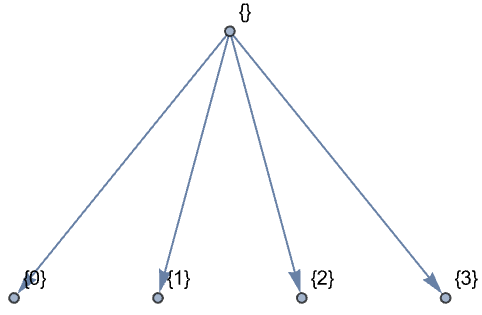
StationaryWaveletPacketTransformを計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-4fxpz9

ウェーブレット係数の木を見る：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-9rgpx
Out[2]=2

ウェーブレット係数の次元を得る：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-ngfrzh
Out[3]=3

ウェーブレット係数をプロットする：

In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-b9yp0h
Out[4]=4

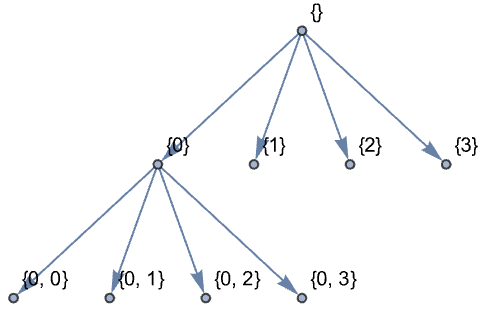
LiftingWaveletTransformを計算する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-6vbut6

ウェーブレット係数の木を見る：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-xwj8z0
Out[2]=2

ウェーブレット係数の次元を得る：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-56ffkm
Out[3]=3

ウェーブレット係数をプロットする：

In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-zrhgbc
Out[4]=4

より高い次元  (1)

多変量スケーリング関数と多変量ウェーブレット関数はそれぞれの一変量関数の積である：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-rk8e1w
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-tvf11
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-yf2o9
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-s16yjj
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0fq4yj0wmxo02-gmiius
Out[5]=5

特性と関係  (16)この関数の特性および他の関数との関係

ローパスフィルタ係数の総和は単位元である．：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-v1t5fi
Out[1]=1

ハイパスフィルタ係数の総和は0である．：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-jrlqqz
Out[2]=2

双対ローパスフィルタ係数の総和は単位元である．：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-80xeur
Out[1]=1

双対ハイパスフィルタ係数の総和は0である．：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-vggc8o
Out[2]=2

スケーリング関数を積分すると単位元になる．：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-3k44bm
Out[1]=1

双対スケーリング関数を積分すると単位元になる．：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-50secc
Out[2]=2

ウェーブレット関数を積分すると0になる．：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-7te20t
Out[1]=1

双対ウェーブレット関数を積分すると0になる．：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-cqbh6v
Out[2]=2

は再帰方程式 を満足する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-yjbxzh
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-i0fiys

構成要素と再帰の総和をプロットする：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-tb4pjl
In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-wvsqxu
Out[4]=4

は再帰方程式 を満足する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-32ph7g
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-lfizfd

構成要素と再帰の総和をプロットする：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-pv65od
In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-siy44p
Out[4]=4

は再帰方程式 を満足する：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-sr719e
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-761w33

構成要素と再帰の総和をプロットする：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-bdrs22
In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-ckzrbh
Out[4]=4

は再帰方程式 を満足する：

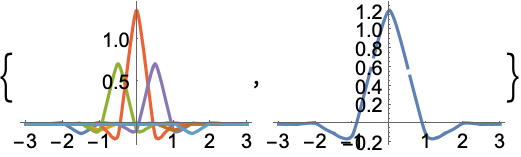
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-4xlw98
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-seqsk7

構成要素と再帰の総和をプロットする：

In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-or3keu
In[4]:=4
✖
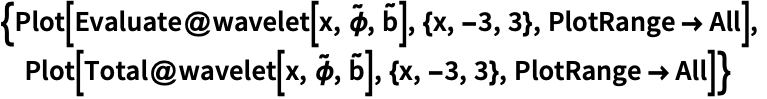
https://wolfram.com/xid/0fq4yj0wmxo02-n5sx2h
Out[4]=4

に対する周波数応答は で与えられる：

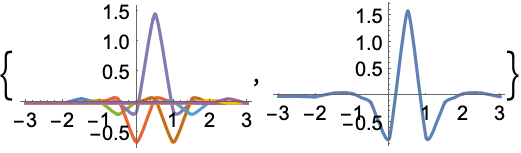
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-y5x0mm

フィルタはローパスフィルタである：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-za6vn3
Out[2]=2

Fのフーリエ(Fourier)変換は で与えられる：

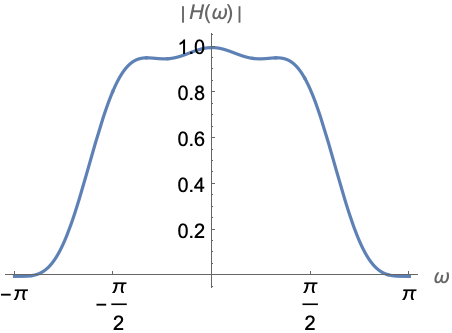
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-idptzz
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-4mxsvj
In[3]:=3
✖
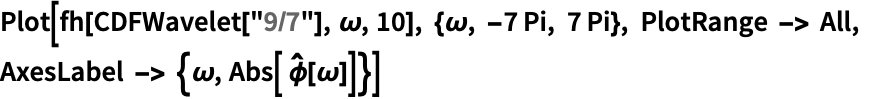
https://wolfram.com/xid/0fq4yj0wmxo02-i4smhk
Out[3]=3

に対する周波数応答はで与えられる：

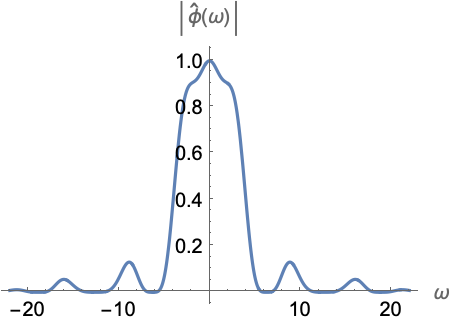
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-n4u9y2

フィルタは双対ローパスフィルタである：

In[2]:=2
✖
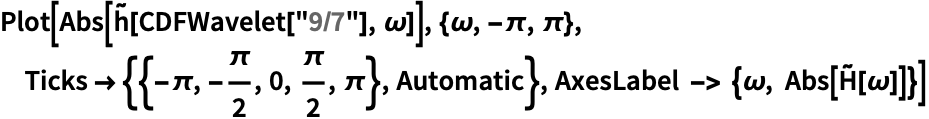
https://wolfram.com/xid/0fq4yj0wmxo02-jod7ab
Out[2]=2

のフーリエ変換はで与えられる：

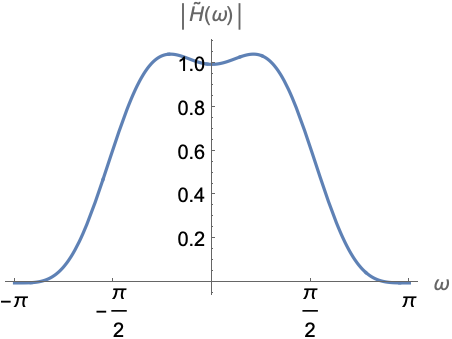
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-le5e5v
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-qp24bt
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-ofeok2
Out[3]=3

に対する周波数応答はで与えられる：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-6u603k

フィルタはローパスフィルタである：

In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-3n6ywg
Out[2]=2

のフーリエ変換は で与えられる：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-b8inb0
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-vsncry
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-h8wifj
In[4]:=4
✖
https://wolfram.com/xid/0fq4yj0wmxo02-rzs5ol
Out[4]=4

に対する周波数応答はで与えられる：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-sjcfi0

フィルタはローパスフィルタである：

In[2]:=2
✖
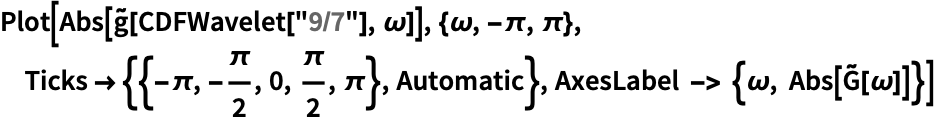
https://wolfram.com/xid/0fq4yj0wmxo02-my0oxb
Out[2]=2

のフーリエ変換は で与えられる：

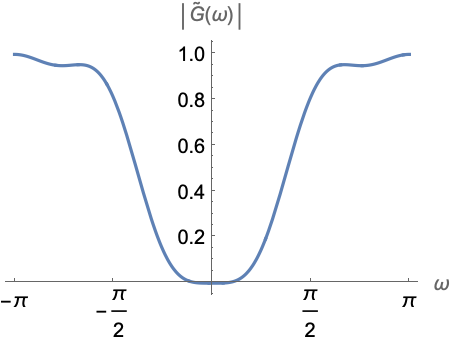
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-69ezed
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-go2zbw
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-53vj8h
In[4]:=4
✖
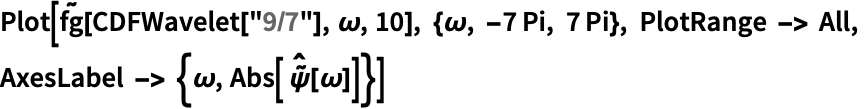
https://wolfram.com/xid/0fq4yj0wmxo02-eytnvi
Out[4]=4

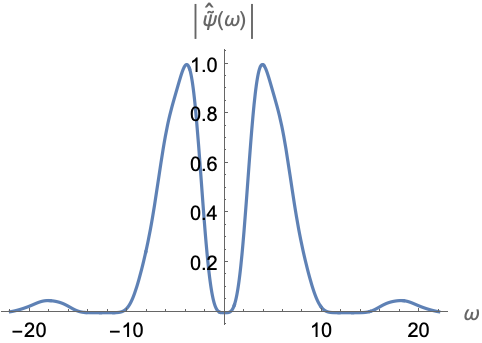
おもしろい例題  (2)驚くような使用例や興味深い使用例

スケーリング関数の平行移動と膨張をプロットする：

In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-yz9dxl
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-evsjio
Out[2]=2
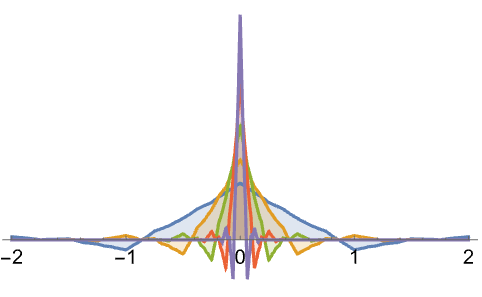
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-p5xgws
Out[3]=3

ウェーブレット関数の平行移動と膨張をプロットする：

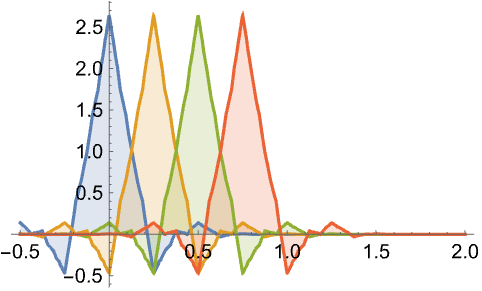
In[1]:=1
✖
https://wolfram.com/xid/0fq4yj0wmxo02-iu0uje
In[2]:=2
✖
https://wolfram.com/xid/0fq4yj0wmxo02-b9ooxs
Out[2]=2
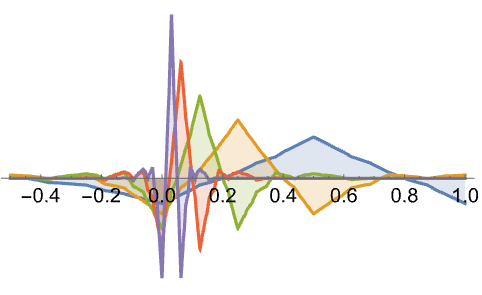
In[3]:=3
✖
https://wolfram.com/xid/0fq4yj0wmxo02-hts69i
Out[3]=3
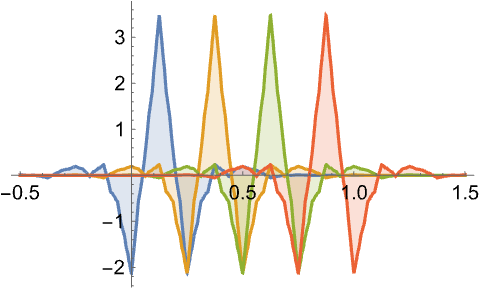
Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.
✖
Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.

テキスト

Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.

✖
Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.

CMS

Wolfram Language. 2010. "CDFWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CDFWavelet.html.

✖
Wolfram Language. 2010. "CDFWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CDFWavelet.html.

APA

Wolfram Language. (2010). CDFWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CDFWavelet.html

✖
Wolfram Language. (2010). CDFWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CDFWavelet.html

BibTeX

@misc{reference.wolfram_2025_cdfwavelet, author="Wolfram Research", title="{CDFWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CDFWavelet.html}", note=[Accessed: 11-July-2025 ]}

✖
@misc{reference.wolfram_2025_cdfwavelet, author="Wolfram Research", title="{CDFWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CDFWavelet.html}", note=[Accessed: 11-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_cdfwavelet, organization={Wolfram Research}, title={CDFWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/CDFWavelet.html}, note=[Accessed: 11-July-2025 ]}

✖
@online{reference.wolfram_2025_cdfwavelet, organization={Wolfram Research}, title={CDFWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/CDFWavelet.html}, note=[Accessed: 11-July-2025 ]}