CaputoD

CaputoD[f,{x,α}]

関数 のCaputo非整数階微積分を与える．

詳細とオプション

  • CaputoDは f のCaputo非整数階微積分として知られている．
  • CaputoDはDを非整数階に一般化して微積分の微分と積分の概念を統一したものである．
  • CaputoDは非整数階微分方程式について初期値問題を使ったシステムのモデリングに広く応用されている．
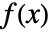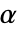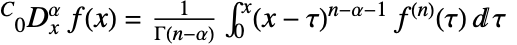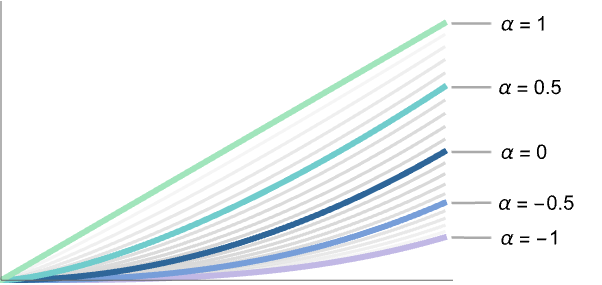
  • の 階の非整数階微分は と定義される．ここで，n=max(0,TemplateBox[{alpha}, Ceiling])である．
  • 分数階微分は，以下で示す関数 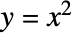とその分数階微分（階数 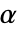は n=max(0,TemplateBox[{alpha}, Ceiling])のとき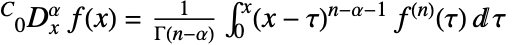 と定義される）のように整数階の微分の間を「補間」する．
  • Caputo非整数階微分は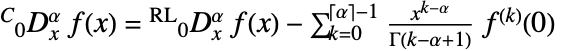を介してFractionalD (リーマン・リウヴィル(Riemann–Liouville)分数階微分）と関連がある．
  • 非整数階微分の階数 α は記号でも任意の実数でもよい．
  • CaputoD[{array},{x,α}]はCaputoDを array の各要素に縫い込む．
  • CaputoDは入力関数のパラメータについては異なるAssumptionsを取る．
  • 与えられた変数 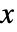に明示的に依存しない式はどれも定数であると解釈される．

例題

すべて開くすべて閉じる

例  (4)

二次関数のCaputo1/2階微分を x について計算する：

二次関数の x についての任意階数のCaputo非整数階微分：

異なる について非整数階微分をプロットする：

正の値についての定数の x についてのCaput非整数階微分は0である：

MittagLefflerEのCaputo非整数階微分：

スコープ  (4)

Exp関数の x についてのCaputo非整数階微分：

Sin関数の x についてのCaputo非整数階微分：

この式はさらに簡約できる：

BesselJ関数のCaputo非整数階微分：

一般系のCaputoD関数のラプラス変換：

Sinにこの式を適用する：

SinのCaputoDにLaplaceTransformを適用して同じ結果を得る：

オプション  (1)

Assumptions  (1)

CaputoDはConditionalExpressionを返すことがある：

Assumptionsを使ってパラメータを制限すると出力が簡約される：

アプリケーション  (8)

三次関数のCaputo1/2階微分を計算する：

Caputo1/2階微分を繰り返して三次関数の通常の微分を得る：

Caputo非整数階積分操作を使ってもとの関数を回復する：

半階Caputo微分を含む微分方程式の非整数階微分を解く：

初期条件を加える：

解をプロットする：

非整数階微分方程式を解く：

解をプロットする：

混合非整数階微分積分方程式を解く：

階数が異なる2つのCaputo微分を含む微分方程式の非整数階微分を解く：

関数のCaputoD非整数階微分を含む2つの微分方程式系を解く：

解を確かめる：

解のパラメトリックプロット：

ベクトル形式の2つの非整数階微分方程式の系を解く：

解をプロットする：

解をパラメータ的にプロットする：

ベクトル形式の3つの非整数階微分方程式系を解く：

解をプロットする：

解をパラメータ的にプロットする：

特性と関係  (7)

CaputoDはすべての実数 について定義される：

Caputo0階微分は関数それ自体である：

CaputoDは複素階数 については定義されない：

定数のCaputo非整数階微分は，正の非整数階については0である：

一般的な規則は以下の通りである：

CaputoDは，すべての負の階数 についてFractionalDと一致する：

FractionalDの出力と比較する：

階数 を負の値に限定すると，CaputoDは自動的にFractionalDの出力を生成する：

ある時点における関数のCaputo非整数階微分を計算する：

よりはやく数値計算を行うためにNCaputoD関数を使う：

考えられる問題  (1)

CaputoD非整数階微分は非整数階によっては定義されないかもしれない：

定義されるものもある：

おもしろい例題  (1)

いくつかの特殊関数について，Caputo1/2階微分の表を作成する：

Wolfram Research (2022), CaputoD, Wolfram言語関数， https://reference.wolfram.com/language/ref/CaputoD.html.

テキスト

Wolfram Research (2022), CaputoD, Wolfram言語関数， https://reference.wolfram.com/language/ref/CaputoD.html.

CMS

Wolfram Language. 2022. "CaputoD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CaputoD.html.

APA

Wolfram Language. (2022). CaputoD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CaputoD.html

BibTeX

@misc{reference.wolfram_2024_caputod, author="Wolfram Research", title="{CaputoD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/CaputoD.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_caputod, organization={Wolfram Research}, title={CaputoD}, year={2022}, url={https://reference.wolfram.com/language/ref/CaputoD.html}, note=[Accessed: 24-November-2024 ]}