FractionalD

FractionalD[f,{x,α}]

gives the Riemann–Liouville fractional derivative of order α of the function f.

Details and Options

  • FractionalD is also known as the Riemann–Liouville differintegral of f.
  • FractionalD generalizes D to fractional order and unifies the notions of derivatives and integrals from calculus.
  • FractionalD plays a foundational role in fractional calculus since other types of fractional derivatives such as CaputoD can be defined in terms of it.
  • The Riemann–Liouville fractional derivative of 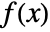of order 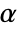is defined as 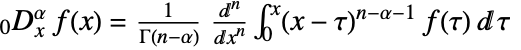, where n=max(0,TemplateBox[{alpha}, Ceiling]).
  • The derivatives of fractional order "interpolate" between the derivatives of integer orders, as shown below for the function 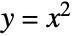and its fractional derivatives of order 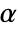given by 2/TemplateBox[{{3, -, alpha}}, Gamma] x^(2-alpha) for :
  • The order α of a fractional derivative can be symbolic or an arbitrary real number.
  • FractionalD[array,{x,α}] threads FractionalD over each element of array.
  • FractionalD takes different Assumptions on the parameters of input functions.
  • All expressions that do not explicitly depend on the given variable are interpreted as constants.

Examples

open allclose all

Basic Examples  (4)

Calculate the half-order fractional derivative of a quadratic function with respect to x:

Arbitrary-order fractional derivative of a quadratic function with respect to x:

Plot these fractional derivatives for different 's:

Calculate the -order fractional derivative of a constant with respect to x:

Fractional derivative of MittagLefflerE:

Scope  (8)

Fractional derivative of the power function with respect to x:

0.23-order fractional derivative of the Exp function with respect to x:

For positive integer , the fractional Riemann–Liouville derivative coincides with the ordinary derivative:

For negative integer , FractionalD differs from the ordinary indefinite integral by a constant:

Fractional derivatives of Sin function are written in terms of HypergeometricPFQ:

Fractional derivatives of BesselJ function:

Fractional derivatives of MeijerG function are given in terms of another MeijerG function:

Laplace transform of a fractional integral in general form:

Substitute the exponential function:

Get the same result by applying LaplaceTransform to the FractionalD of Exp:

Options  (1)

Assumptions  (1)

FractionalD may return a ConditionalExpression:

Restricting parameters using Assumptions will simplify the output:

Applications  (2)

Calculate the half-order fractional derivative of the cubic function:

Get the ordinary derivative of the cubic function repeating the half-order fractional differentiation:

Recover the initial function using fractional integration:

Consider the following fractional order integral equation:

Solve it for the Laplace transform:

Find the inverse transform:

Verify this solution:

Properties & Relations  (6)

FractionalD is defined for all real :

The 0-order fractional derivative of a function is the function itself:

FractionalD is not defined for complex order :

In general, the fractional derivative of a constant is not 0:

FractionalD results may contain DifferenceRoot sequences:

This general expression is simplified to a finite sum of HypergeometricPFQ instances if is a given real number:

Calculate the fractional derivative of a function at some point:

Use the NFractionalD function for faster numerical calculations:

Neat Examples  (1)

Create a table of α^(th) fractional and n^(th) ordinary derivatives of a few special functions:

Wolfram Research (2022), FractionalD, Wolfram Language function, https://reference.wolfram.com/language/ref/FractionalD.html.

Text

Wolfram Research (2022), FractionalD, Wolfram Language function, https://reference.wolfram.com/language/ref/FractionalD.html.

CMS

Wolfram Language. 2022. "FractionalD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalD.html.

APA

Wolfram Language. (2022). FractionalD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FractionalD.html

BibTeX

@misc{reference.wolfram_2025_fractionald, author="Wolfram Research", title="{FractionalD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/FractionalD.html}", note=[Accessed: 30-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fractionald, organization={Wolfram Research}, title={FractionalD}, year={2022}, url={https://reference.wolfram.com/language/ref/FractionalD.html}, note=[Accessed: 30-July-2025 ]}