WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

PoissonPointProcess
✖
PoissonPointProcess

[Experimental]

✖

represents a homogeneous Poisson point process with constant intensity μ in .

Details

  • PoissonPointProcess is also known as homogeneous Poisson point process, stationary Poisson point process and complete spatial randomness (CSR).
  • PoissonPointProcess generates points that are uniformly distributed in a region, with the average number of points per unit volume equal to μ.
  •     
  • Typical uses are to model and test point collections that are completely spatially random. They are frequently used as building blocks for more complicated point processes such as clustered point processes.
  • With intensity μ, the number of points in the observation region with volume follows the distribution PoissonDistribution[μ ν].
  • The number of points in disjoint regions 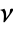for a Poisson point process consists of independent random variables so 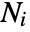. This property is also referred to as complete spatial randomness (CSR).
  • A point configuration 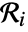with intensity μ in an observation region 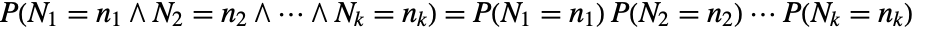with volume has density function 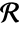with respect to PoissonPointProcess[1,d].
  • The Papangelou conditional density 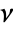for adding a point 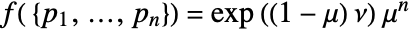to a point configuration 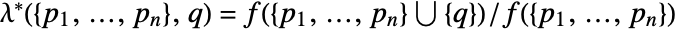is 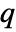for a Poisson point process with intensity μ.
  • PoissonPointProcess allows μ to be any positive real number and d to be any positive integer.
  • Possible PointProcessEstimator settings in EstimatedPointProcess for PoissonPointProcess are:
  • Automaticautomatically choose the parameter estimator
    "MaximumPseudoLikelihood"maximize the pseudo-likelihood
  • PoissonPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Sample from a Poisson point process:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-4mqsf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-d381by
Out[2]=2

Sample a Poison point process with several realizations:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-gwc84f
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-hdfqz
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-hc6ki4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-bi5nn
Out[4]=4

Simulate Poisson point process over a country:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ex5gf5
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-cdzemc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-valcig
Out[3]=3

Scope  (4)Survey of the scope of standard use cases

Sample a Poisson point process from any valid region whose RegionEmbeddingDimension is equal to its RegionDimension:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-qxrhco

Check the region conditions:

In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-pacet0
Out[2]=2

Sample points from the region:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ydq337
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-h8cla8
Out[4]=4

Sample from PoissonPointProcess using the different methods:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-8j1bt
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-qr7z0c

Use thinning method:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-8i748x
Out[3]=3

Use Markov chain Monte Carlo method:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-r8z4hx
Out[4]=4

Plot samples over the region:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-mhakyk
Out[5]=5

Estimate PoissonPointProcess:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-4k0ip
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-gltjpq
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-18qtuz
Out[3]=3

Estimate PoissonPointProcess over a geo region:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-d1ac2x
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zal2if
Out[5]=5

Convert to metric units:

In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-fgu7eu
Out[6]=6

Find PointCountDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zw29h5
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-tdcfpk
Out[2]=2

For a geo case:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-7er7zr
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-n9rxt8
Out[4]=4

Applications  (3)Sample problems that can be solved with this function

Suppose flaws in plywood occur on an average of one flaw per 50 square feet. Simulate the process of finding flaws on a per-square-foot basis:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-fz5csd
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-6ye4y3
Out[4]=4

Find the probability that a 4-foot×8-foot sheet will have no flaws:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-rm916e
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-sknjp
Out[6]=6

For a round mirror with area 7.54 cm^2, the probability of no flaws is 0.91. Using the same polishing process, another round mirror with an area of 19.50 cm^2 is fabricated. Assuming the flaws are independent and randomly located, find the probability of no flaws on the larger mirror:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-cewm1r
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-6w5afw

Find the intensity of the flaw point process:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-yj47q0
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-lf0rpd
Out[4]=4

The resulting mirror polishing defect process is then:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ynqos8
Out[5]=5

The probability of no errors in the larger mirror:

In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-wam2ku
In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zt1f38
Out[7]=7

An LCD display has 1920×1080 pixels. A display is accepted if it has 15 or fewer faulty pixels. The probability that a pixel is faulty from production is and the faulty pixel positions are independent and random. Find the proportion of displays that are accepted:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-s3tyax
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-x7g8uw

Simulate the faulty pixel configuration:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-8caypb
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-2y2hva
Out[4]=4

Find the probability of no more than 15 faulty pixels in the display:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-b339un
Out[5]=5

Find the pixel failure rate required to produce 4000×2000 pixel displays and still have an acceptance rate of at least 90%:

In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-gvrjx3
In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-m1rnsy
Out[7]=7

Plot the acceptance rate as a function of the pixel failure rate:

In[8]:=8
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-lkxmue
Out[8]=8

Find the maximal acceptable pixel failure rate:

In[9]:=9
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-n5i27z
Out[9]=9

Check the result:

In[10]:=10
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-fakpmz
Out[10]=10

Properties & Relations  (11)Properties of the function, and connections to other functions

The number of points in a PoissonPointProcess is Poisson distributed:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-hetb1
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-czqwet
Out[2]=2

Simulate a PoissonPointProcess over a unit disk:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-usnk9
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-jjyqjn
Out[5]=5

Distribution of point counts:

In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-m8ilnh
Out[6]=6

Compare the histogram of point counts with the PDF:

In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-c7nyut
Out[8]=8

Fit a PoissonDistribution to the point counts:

In[9]:=9
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-gr4k9c
Out[9]=9

Test goodness of fit:

In[10]:=10
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-m46usn
Out[10]=10

Test against the underlying distribution:

In[11]:=11
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-bk6ev7
Out[11]=11

Compute void probabilities for a Poisson point process. For a disk:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-60ixxo
Out[1]=1

For a rectangle:

In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-fwyxlc
Out[2]=2

For a unit ball:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-t91rcu
Out[3]=3

The probability of finding a point within distance of an arbitrary location:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-nh7u6b
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-kdmuk4
Out[2]=2

This equivalent to the CDF of RayleighDistribution:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-xhg94s
Out[3]=3

Equivalently compute SurvivalFunction at 0 of PointCountDistribution:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-02en7s
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-waz3gk
Out[5]=5

Poisson point process is stationary—the intensity is translation invariant:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-fugl3p

Point count distribution in a subregion:

In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-em07kv
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-p79axg
Out[3]=3

Point count distribution in the translated subregion:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-1nahei
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-kr3wtf
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-df06jd
Out[6]=6

Poisson point process is isotropic—the intensity is rotation around origin invariant:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-prr8pq

Point count distribution in a subregion:

In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-76dbja
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ncu7es
Out[3]=3

Point count distribution in the translated subregion:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-l1ywun
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-qcgl5a
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-5o7bro
Out[6]=6

PoissonPointProcess has the property of complete spatial randomness:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-drz1qm
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zycwk7
Out[2]=2

Define left and right half-disks:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-iwogu8

Create subset of points in each subregion:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-jnxpnh
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-jpop5
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ejv1bz
Out[6]=6

Extract the number of points for each subregion:

In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-z5ve2v

Test whether two samples are independent:

In[8]:=8
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-z67hm1
Out[8]=8
In[9]:=9
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-pcac3h
Out[9]=9

Ripley's function for the Poisson point process has closed form and does not depend on the intensity:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-3hltk1
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-m6387j
Out[2]=2

Plot the function for few dimensions:

In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-8g4nyq
Out[3]=3

Besag's for the Poisson point process does not depend on intensity or dimensionality:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zht24f
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-myijw0
Out[2]=2

PairCorrelationG for the Poisson point process is constant:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-o75yfs
Out[1]=1

EmptySpaceF and NearestNeighborG functions of a Poisson point process are identical:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ezl23u
In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-peicch
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-s1mw7o
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-iuhnsy
Out[4]=4

They both are equivalent to the CDF of an ExponentialDistribution:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-tk0pll
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-ynkq7r
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-9i3ozc
Out[7]=7

InhomogeneousPoissonPointProcess with a constant intensity function is PoissonPointProcess:

In[1]:=1
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-br72ig

The point count distribution in a disk:

In[2]:=2
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-pahxp9
In[3]:=3
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-zexcc4
Out[3]=3

Point count distribution for a corresponding Poisson point process in the same region:

In[4]:=4
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-4vy82f
Out[4]=4

In higher dimension:

In[5]:=5
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-e9ghmv
In[6]:=6
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-irlzgr

The point count distribution in a ball:

In[7]:=7
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-6kz6no
Out[7]=7

Point count distribution for a corresponding Poisson point process in the same region:

In[8]:=8
✖
https://wolfram.com/xid/0rkimu2nn1r2qwi-bo69a7
Out[8]=8
Wolfram Research (2020), PoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonPointProcess.html.
✖
Wolfram Research (2020), PoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

Text

Wolfram Research (2020), PoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

✖
Wolfram Research (2020), PoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

CMS

Wolfram Language. 2020. "PoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

✖
Wolfram Language. 2020. "PoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonPointProcess.html.

APA

Wolfram Language. (2020). PoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonPointProcess.html

✖
Wolfram Language. (2020). PoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonPointProcess.html

BibTeX

@misc{reference.wolfram_2025_poissonpointprocess, author="Wolfram Research", title="{PoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonPointProcess.html}", note=[Accessed: 27-March-2025 ]}

✖
@misc{reference.wolfram_2025_poissonpointprocess, author="Wolfram Research", title="{PoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonPointProcess.html}", note=[Accessed: 27-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_poissonpointprocess, organization={Wolfram Research}, title={PoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/PoissonPointProcess.html}, note=[Accessed: 27-March-2025 ]}

✖
@online{reference.wolfram_2025_poissonpointprocess, organization={Wolfram Research}, title={PoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/PoissonPointProcess.html}, note=[Accessed: 27-March-2025 ]}