CellularAutomaton

CellularAutomaton[rule,init,t]

セルオートマトンを指定した条件で初期条件 init から t ステップ実行した進化を表すリストを生成する．

CellularAutomaton[rule,init]

1ステップ分の init の進化の結果を返す．

CellularAutomaton[rule,init,{tspec,xspec,…}]

tspec，xspec 等で指定された進化の部分だけを返す．

CellularAutomaton[rule,init,{t,All,…}]

t ステップの間に影響を受けるであろうすべてのセルを各ステップに含む．

CellularAutomaton[rule]

進化の1ステップを表す，CellularAutomatonの演算子形である．

詳細

  • rule の可能な形
  • n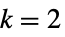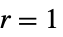，，ルール番号 n の初期ルール
    {n,k}k 色の一般的な最近傍ルール
    {n,k,r}k 色で範囲 r の一般ルール
    {n,k,{r1,r2,…,rd}}d 次元の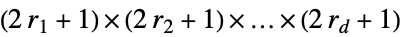近傍ルール
    {n,k,{{off1},{off2},…,{offs}}} 指定のオフセットの近傍ルール
    {n,k,rspec,s}s 次ルール
    {n,{k,1}}k 色の最近傍の総和型ルール
    {n,{k,1},r}k 色で範囲 r の総和型ルール
    {n,{k,{wt1,wt2,…}},rspec}近傍 i に重み wtiが割り当てられているルール
    {lhs1->rhs1,lhs2->rhs2,…}近傍のリストの明示的置換え
    {fun,{},rspec}各近傍のリストに適用する一般関数 f
    bfun近傍集合に適用するブール関数
    CellularAutomaton[rule]規則の演算子形
    <|"key1"val1,"key2"val2,…|>連想によるルール指定
    "name"名前付きルール
  • CellularAutomaton[{n,k},…]はCellularAutomaton[{n,{k,{k^2,k,1}}},…]に等しい．
  • 次のキーを使って連想として与えられるルールを指定することができる．
  • "RuleNumber"nルール番号
    "TotalisticCode"n総和型コード
    "OuterTotalisticCode"n外部総和型コード
    "GrowthCases"{g1,g2,…}近傍の giが1の時，セル1を作る
    "GrowthSurvivalCases"{{g1,…},{s1,…}}giの近傍は1で siについては変更しない
    "GrowthDecayCases"{{g1,…},{d1,…}}giの近傍は1で diについては0
    "Dimension"d全体的な次元
    "Colors"k色の数
    "Range"rルールの範囲
    "Neighborhood"type近傍タイプ
  • "GrowthCases"->{g1,g2,…}のとき，セルに1である gi近傍がある場合は，そのセルは値0から値1に変化する．それ以外の場合は，そのセルは前と同じままである．
  • "GrowthSurvivalCases"->{{g1,…},{s1,…}}のとき，セルに1である gi近傍がある場合は，そのセルは値0から値1に変化し，1である si近傍がある場合は値1を保持する．それ以外の場合は値が0になる．
  • "GrowthDeathCases"->{{g1,…},{d1,…}}のとき，セルに1である gi近傍がある場合は，値0から値1に変化する．1である di近傍がある場合は値0を得る．それ以外の場合は同じ状態に止まる．
  • 次は，2Dにおける"Neighborhood"の可能な設定である．
  • 5 または "VonNeumann"CrossMatrix[1]
    9 または "Moore"BoxMatrix[1]
  • 次元 d のとき，"Neighborhood"は整数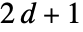および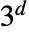と同様に"VonNeumann"および"Moore"をサポートする．
  • 次は，CellularAutomaton["name",…]として与えることのできる名前付きセルオートマトンルールである．
  • "Rule30"30
    "Rule90"90
    "Rule110"110
    "Code1599"{1599,{3,1}}
    "GameOfLife"{224,{2,{{2,2,2},{2,1,2},{2,2,2}}},{1,1}}
  • 二次元のセルオートマトンルールのよくある明示的一般形
  • {n,{k,1},{1,1}}9近傍の総和型ルール
    {n,{k,{{0,1,0},{1,1,1},{0,1,0}}},{1,1}}
    5近傍の総和型ルール
    {n,{k,{{0,k,0},{k,1,k},{0,k,0}}},{1,1}}
    5近傍の外部総和型ルール
  • セルオートマトンの可能な規則の数は次の通りである．
  • 初期ルール256
    一次元一般ルール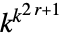
    一次元総和型ルール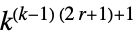
    二次元一般ルール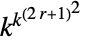
    二次元9近傍総和型ルール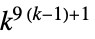
    二次元5近傍総和型ルール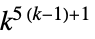
    二次元5近傍外部総和型ルール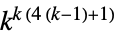
  • 一般に，initと進化のリストの全要素はゼロから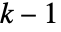までの整数である．
  • 一般関数または置換えリストが用いられる場合は，init と進化のリストの要素は任意の式でよい． »
  • 明示的な置換規則の lhsi->rhsiにはパターンが含まれている．
  • 一次元セルオートマトンの場合，置換規則や明示的な関数 fun は常に近傍の一次元リストに適用されると解釈される．近傍が明示的なオフセットで指定されている場合，その近傍はオフセットの順に与えられる．
  • 多次元セルオートマトンにおける近隣が{r1,r2,…}のような範囲指定で定義されている場合，近傍のリストは次元が2{r1,r2,…}+1の完全配列であると解釈される．
  • 多次元セルオートマトンの近傍がオフセットの明示的なリストで指定されている場合，その近傍は一次元のリストにオフセットの順序で与えられる．
  • 明示的な関数 fun が与えられた場合，この関数の第1引数は近傍のリストである．第2引数は0から始まるステップ数である．
  • 完全なルール指定は，BooleanVariables[bfun]が整数 v を返す場合は，純ブール関数 bfun であるとみなされる．この場合，bfun は各ステップの v 個のセルの近傍に適用される．近傍は左側のCeiling[v/2]個のセルまで拡張される．
  • {rule,kspec,rspec,s}で指定される s 次のセルオートマトンでは，各ステップが s 個前のステップに依存する．
  • 初期条件は以下のように init によって設定される．
  • {a1,a2,…}周期的であると考えられる，値 ai の明示的なリスト
    {{a1,a2,…},b}背景 b に重ねられた値 ai
    {{a1,a2,…},{b1,b2,…}}b1, b2, …の反復である背景に重ねられた値 ai
    {{{{a11,a12,…},off1}, {{a21,…},off2},…},bspec}
    背景上のオフセット offi の値 aij
    {{a11,a12,…},{a21,…},…}二次元の値の明示的リスト
    {aspec,bspec}d 次元で d 次元のパディングを伴う値
  • aspec の第1要素は，各座標で原点に対して正の方向に最初の位置で背景に重ねられる．つまり，bspec[[1,1,…]]はaspec[[1,1,…]]と並ぶことになる．
  • CellularAutomaton[rule,init,t]は，長さ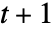の進化リストを生成する．
  • s 次のセルオートマトンについては，init がシステムの進化における最初の s ステップを与えるリストである．
  • {tspec,xspec,…}における時間指定 tspec は次のようにできる．
  • t0から t までの全ステップ
    {t}t ステップしか含まないリスト
    {{t}}ステップ t のみ
    {t1,t2}t1 から t2 までのステップ
    {t1,t2,dt}ステップ t1, t1+dt, …
  • 初期条件はステップ0であると考えられる．
  • CellularAutomaton[rule,init,{tspec}]は，xspec にデフォルトのAutomaticを使う．
  • 空間指定 xspec は次のようにできる．
  • All指定された初期条件に影響されるすべてのセル
    Automatic領域内の背景と異なるすべてのセル
    0aspec の始めと並んでいるセル
    x右側に最大 x のオフセットを持つセル
    -x左側に最大 x のオフセットを持つセル
    {x}右側に x のオフセットを持つセル
    {-x}左側に最大 x のオフセットを持つセル
    {x1,x2}x1 から x2 までのオフセットを持つセル
    {x1,x2,dx}x1, x1+dx, …のセル
  • 一次元では aspec の最初の要素はデフォルトで空間オフセット0を持つとされる．
  • 何次元であっても，aspec[[1,1,1,…]]はデフォルトで空間オフセット{0,0,0,…}を持つとされる．
  • CellularAutomatonで作成される進化リストの各要素は常に同じサイズである．
  • 幅 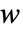の aspec によって指定される初期条件により，領域 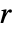の規則を持つセルオートマトンの 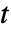ステップ後に影響を受ける領域は幅 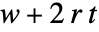になる．
  • 背景 bspec が指定されていなければ，AllとAutomatic空間オフセットは aspec にあるすべてのセルを含む．
  • Allの空間オフセットは初期条件の影響を受けるすべてのセルを含む．
  • Automaticの空間オフセットはセルオートマトンのパターンの側面から背景をカットするために使うことができる．
  • どれくらいの領域を保持すればよいかを決める際，Automaticは offt で指定したステップの結果のみを使う．
  • CellularAutomaton[rule][init]は，CellularAutomaton[rule,init]と等価である．

例題

すべて開くすべて閉じる

例  (3)

ルール30を2ステップ実行する：

0を背景とし単一の1から始めて50ステップ実行する：

セルオートマトンルールのアイコンを生成する：

スコープ  (91)

一次元ルール  (26)

初期ルール73：

RulePlotを使って同じ結果を生成する：

3色ルール679458：

ルールアイコンを生成する：

3色総和型ルール，コード867：

範囲 （左に2近傍，右に1近傍）の2色ルール23898：

一般範囲 ルール：

の総和型ルール（コード10）：

近隣のセルに明示的なオフセットを与えることによって指定されたルール30：

オフセットを変更したルール30に類似の規則：

2近傍のルール：

近隣セルに明示的な重みを与えることで指定したルール30：

3色の総和型ルール：

総和型ルールでは，近隣の各オフセットが重み1を持つ：

3色の外部総和型ルール：

近傍に明示的な置換を与えてルール90を指定する：

単一の「代数的な」置換規則を与えることでルール90を指定する：

TrueおよびFalseという状態に作用する明示的なブール公式をルール30に適用する：

セルオートマトン中の値は任意の記号式でよい：

範囲1の近傍に適用する規則として任意の記号関数fを使う：

オフセットがとの近傍に関数を適用する：

「パスカル(Pascal)の三角形のセルオートマトン」を設定する：

明示的な関数としてルール90を指定する：

4を法とした付加的なセルオートマトン：

関数の第2引数はステップ数である：

連続するステップで規則を変更する．#2はステップ数である：

セルの連続する値を使う：

ルール90を純ブール関数として指定する：

ルール90の の類推は純ブール関数を使って指定される：

連想で指定されたルール  (5)

連想を使ってルール30を指定する：

3色のセルオートマトン：

2色で範囲が3/2のセルオートマトン：

3色の総和型セルオートマトン：

3色の外部総和型セルオートマトン：

初期条件  (8)

明示的な初期条件は循環的であると想定される：

最も左側のセルの左近傍は最も右側のセルであり，逆もまた真である：

ランダムな初期条件：

0に囲まれたブロック1101からなる「シード」から始める：

1に囲まれた単独の0から始める：

10個のブロックを繰り返す背景上の111から始める：

「シード」を疎な配列として指定する：

SparseArrayを使って完全に循環的な初期条件を与える：

オフセットのブロック101とオフセットのブロックから始める：

タイムステップ  (6)

進化の2ステップ：

別の形：

第2ステップのみを含むリスト：

リストにはない第2ステップ：

50番目から80番目までのステップ：

初期条件はステップ0である：

0番目から100番目まで，3つおきのステップを示す：

範囲指定  (11)

デフォルトで，CellularAutomatonはパターンでカバーされない範囲を自動的に削除する：

これと等価の形：

規則の枠組みを与えられると影響を受ける可能性があるすべてのセルを含む：

背景とは違う範囲だけを含む：

影響を受ける可能性があるすべてのセルを含ませる：

デフォルトで，規則が違うと与えられる範囲の幅も異なる：

同じ型のすべての規則が同じ幅の範囲を与えるように強制する：

影響を受ける可能性がある範囲は規則の範囲による：

セル0（最初の1の位置）からセル40までの範囲だけを示す：

負の位置は左になる：

各ステップがセル0だけからなる範囲を与える：

セル0の値だけを含み，リストには含まれない：

時間と空間で1つおきのセルだけを示す：

セル0は常に，初期条件の明示的部分で最も左側になる：

有限ブロックを反復して位置からまでの初期条件の範囲を埋める：

多次元ルール  (13)

範囲1の二次元（9近傍）総和型コード14を2ステップ実行する：

2ステップ後の結果だけを与える：

30ステップ後の結果を示す：

各セルの平均色を示す：

時間的空間的履歴を3D画像として表示する：

各1セルの位置で立方体を示す：

オフセット0で におけるすべての の値についての50ステップの時空スライス：

特定の の位置におけるすべてのセルの平均的な色：

RulePlotを使って総和型ルール指定を可視化する：

5近傍総和型ルール：

5近傍外部総和型ルール：

RulePlotを使って外部総和型ルール指定を可視化する：

疎な配列内で指定された2つの黒いセルを持つ初期条件を使う：

三次元最近傍総和型セルオートマトン：

連想による多次元ルール指定  (8)

連想を使って2D総和型コード14を指定する（9セル近傍を仮定）：

5近傍総和型コード26：

文字列"VonNeumann"を使って近傍を説明する：

5近傍外部総和型コード110：

セルに値1の（9つのうち）1つまたは2つの近傍があるときにそのセルが値1を得る成長ルール：

3D画像：

値1の近傍を1つまたは2つ持つセルに値1が与えられ，値1の近傍が6つまたは7持つセルには値0が与えられる成長崩壊ルール：

値1の近傍が1つまたは2つあるセルに値1が与えられ，値1の近傍が6つまたは7つあるセルはそのままの状態に置かれ，その他の場合にはセルに値0が与えられるルール：

7近傍のうちの1近傍の値が1のときにセルの値が1になるルール：

27の近傍のうち1近傍の値が1のときにセルの値が1になるルール：

高階ルール  (6)

ルール30は明示的に「一階ルール」として書き出される：

初期条件の2ステップを含むルール30に相当する二階ルール：

出力に両方の初期条件ステップを含む：

二階ルール1008は，両方の初期条件ステップで単一の1から始まる：

初期条件に両方のステップを含む：

2色，範囲1の二階総和型ルール10：

同じ規則を12階にしてみる：

ルール150R—二階の反転可能な2を法とする規則：

2色範囲1の二階総和型ルールの時空スライス：

同じ規則のステップ50：

関数バージョン  (6)

ルール30の1ステップの進化の結果を与える：

上とは別の形：

単一ステップを3回繰り返す：

3ステップの進化の結果を与える：

繰り返される背景に囲まれた中央部分として結果を与える：

ルール45は1ステップの後1による背景を与える：

ルール45の単一ステップを繰り返す：

規則を演算子形で指定する：

文字列で指定された特殊ルール  (2)

文字列として指定されたルール30：

文字列を使って指定されたライフゲームのルール：

アプリケーション  (23)

ルール30のカラー画像を作成する：

最初の32の一次元セルオートマトンの画像を作成する：

2色で範囲が2の総和型コード20のセルオートマトンを一連の初期条件から示す：

異なる初期条件での3色で範囲が3の総和型コード1599の結果を示す：

各パターンの端を3つの0で充填する：

単一の進化を複数の「パネル」で示す：

ルール30の200ステップを示す：

ルール30の中央列のセルの値から「ランダム」ウォークを作成する：

連続する幅の循環的領域におけるルール90の繰返し周期を求める：

サイズ7の領域でルール110の状態遷移のグラフを描く：

初期条件が1ビット異なる2つのセルオートマトンについて異なるパターンを生成する：

共通の進化は灰色で示す：

外部総和型2Dセルオートマトンを使って迷路のような模様を生成する：

成長ルールを使って不規則なパターンを生成する：

5近傍外部総和型2Dセルオートマトンの進化のステップを示す：

「ライフゲーム」の「グライダー」を示す：

「ライフゲーム」の「汽車ぽっぽ」の進化を示す：

ランダムな初期条件からの「ライフゲーム」，平均100ステップ：

平均した時空スライス：

二次元の9近傍ルールの連続によって生成したパターン：

中央セルの値：

二次元セルオートマトンの進化を球体を使って3Dで描画する：

三次元セルオートマトンの進化におけるステップの連続を示す：

三次元セルオートマトンの高さの連続におけるスライスの時間平均を示す：

パスカル(Pascal)の三角形を構築する：

複素整数の乗算に基づいたセルオートマトン：

3を法とする加法規則を代数的に簡約する：

特性と関係  (9)

メッシュラインを含む：

セルにラベルを付ける：

セルの中央列をハイライトする：

RulePlotを使ってグラフィックスを生成する：

Imageは各セルが1画素の画像を生成する：

ステップのセルオートマトンの進化のリストの長さは になる：

明示的なリストとして与えられた初期条件は循環的であるとみなされる：

可能なすべてのタプルから始まる中央セルはルール番号の桁数を与える：

次は，5近傍外部総和型コードである：

このRulePlotを生成する：

これと等価のルールは成長生存形式である：

成長崩壊形式におけるルール：

考えられる問題  (7)

デフォルトでは，各進化のリストは必要な長さにしか作成されない：

{t,All}を使って，特定の型のすべての規則について同じ長さのリストを得る：

背景と異なるセルがない場合は，自動的に選ばれた範囲は常に空白となる：

代替となる背景を持つ規則は，0だけを含むリストを与えることができる：

進化が2ステップ続けられた場合は，1ステップの結果に明示的な1が含まれる：

この形式では，背景指定が含まれる：

デフォルトでは，各進化は必要なだけの広さしか持たない：

{t,All}を使って一定の幅にする：

3色ルールは値0と1しか生成しないことがある：

ArrayPlotで可視化すると，値1は黒く表示される：

RulePlotを使ってもとになっているルールに従って正しい色で表示する：

明示的なColorRulesを使ってもArrayPlotのデフォルトの問題を避けることができる：

RulePlotを使ってもとになっているルールを示す：

CellularAutomatonのセルとステップは，その部分番号によって番号を付けられる訳ではない：

オフセットが異なる順番で指定されると，ルール番号も異なる意味を持つ：

Wolfram Research (2002), CellularAutomaton, Wolfram言語関数， https://reference.wolfram.com/language/ref/CellularAutomaton.html （2017年に更新）.

テキスト

Wolfram Research (2002), CellularAutomaton, Wolfram言語関数， https://reference.wolfram.com/language/ref/CellularAutomaton.html （2017年に更新）.

CMS

Wolfram Language. 2002. "CellularAutomaton." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/CellularAutomaton.html.

APA

Wolfram Language. (2002). CellularAutomaton. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CellularAutomaton.html

BibTeX

@misc{reference.wolfram_2024_cellularautomaton, author="Wolfram Research", title="{CellularAutomaton}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/CellularAutomaton.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cellularautomaton, organization={Wolfram Research}, title={CellularAutomaton}, year={2017}, url={https://reference.wolfram.com/language/ref/CellularAutomaton.html}, note=[Accessed: 22-November-2024 ]}