CriticalityFailureImportance

CriticalityFailureImportance[rdist,t]

ReliabilityDistribution rdist の時間 t におけるすべての成分のクリティカリティ故障重要度を与える．

CriticalityFailureImportance[fdist,t]

FailureDistribution fdist の時間 t におけるすべての成分のクリティカリティ故障重要度を与える．

詳細

  • CriticalityFailureImportanceは故障致命度あるいはクリティカリティ重要度因子としても知られている．
  • 成分 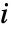のクリティカリティ故障重要度は 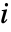成分が系の故障の原因となった確率である．ただし，系は時間 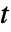で故障するものとする．
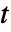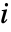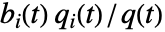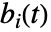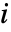  • 時間 における成分 のクリティカリティ故障重要度は で与えられる．ただし， は成分 のBirnbaum重要度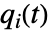，は成分 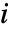が故障した確率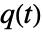，は系が故障した確率である．
  • 結果は rdist または fdist の分布リストでの成分順で与えられる．

例題

すべて開くすべて閉じる

例  (3)

異なる寿命分布を持ち，直接接続された2つの成分：

結果はReliabilityDistributionにおける分布リストと同じ順で与えられる：

並列成分は両方とも系の故障に関係がある：

故障の木に基づいたモデリングを使って系を定義する：

スコープ  (17)

ReliabilityDistributionモデル  (9)

等しい寿命分布を持ち，並列接続された2つの成分：

どちらの成分も同じように系の故障を引き起こす可能性がある：

等しい寿命分布を持ち，直列接続された2つの成分：

どちらの成分も同じように系の故障を引き起こす可能性がある：

寿命分布が等しい3つの成分のうち2つが動作に必要な系：

どの成分についても系の故障の原因になる確率は等しい：

寿命分布が等しい単純な混合系：

重要度を計算する：

成分 が系の故障を引き起こす可能性が最も高い：

1つの成分と並列で接続されている直列接続の系：

重要度を計算する：

故障した系では，成分 が常に故障していた．したがって，これが系の故障を引き起こす確率は1である：

単純な混合系で母数の変更の影響を調べる：

重要度を計算する：

並列成分の一つ， を悪化させたときの重要度の変化を示す：

分布が異なる他の2つと並列接続している1つの成分：

時間のある特定の点における重要性尺度を厳密な結果として求める：

機械精度の結果として：

記号式で：

任意の有効なReliabilityDistributionを使うことができる：

待機成分が系の故障を引き起こした可能性は低い：

部分系の重要性尺度を得るために段階を追って系をモデル化する：

時間に沿って重要度をプロットする：

FailureDistributionモデル  (8)

2つの基本事象のどちらかが頂点事象を引き起こす：

どちらの事象も同じように頂上事象を起こす可能性がある：

両方の基本事象が一緒になるとはじめて頂上事象が引き起こされる：

頂上事象が起った場合，これに貢献した確率は と の両方とも1になる：

基本事象の分布が等しいボーティングゲート：

ボーティングゲートの事象が等しいと頂上事象を引き起こす確率も等しくなる：

AndゲートとOrゲートの両方がある単純な系：

クリティカリティ重要度を計算する：

頂上事象が起ったときは，事象 が常に起っている：

AndゲートとOrゲートの両方がある単純な系：

重要度を示す：

事象 が頂上事象を引き起こした可能性が最も高い：

単純な混合系で母数の変化が与える影響を調べる：

重要度を計算する：

基本事象の一つ， を悪化させた場合の重要度の変化を示す：

任意の有効なFailureDistributionを使うことができる：

待機のモデル化された事象よりもあまり信頼性の高くない事象が，頂上事象を引き起こした可能性が高い：

部分系の重要性尺度を得るために系を段階を追ってモデル化する：

時間に沿って重要度をプロットする：

アプリケーション  (4)

水中のパイプラインの修理は水面下のドライメンテナンスキャビンを使って行われる．このキャビンへの生命維持装置は次の分布に従う：

典型的な作業時間は24時間である．このような作業のクリティカリティ故障重要度を計算する：

指揮官が1人，情報部員が1人，武器，工学，医学，通信の専門員がそれぞれ2名の特殊部隊について考える．この部隊は各分野の専門員が1人いる限り機能すると仮定する：

次の寿命分布を仮定する：

10時間の作戦で成功する確率を計算する：

作戦を失敗に導く可能性が最も高い役割を求める：

結果を重要度でソートする：

情報部員を1人追加することで部隊を強化する：

生存確率が99.6%から99.9%に上がった：

航空機の離陸時の際に故障致命度が最も高い成分は何かを分析する．格納扉は電動・手動のどちらで開けることもできる：

2つの燃料ポンプを動かすためには動力が必要である：

さらに，次の燃料移送構造で，2つのポンプを信頼できる電池を使って動かすことができる：

航空機の除氷装置と燃料の収蔵タンクも必要である：

寿命分布を定義する：

重要度を計算する：

航空機の離陸失敗には燃料貯蔵と動力が最も関係している：

3時間の作業時間の中で最も重要な成分を求める：

時間に沿って重要度を示す：

3時間の作業時間中，成分 が故障を引き起こした可能性が最も高い：

特性と関係  (5)

故障に基づいたクリティカリティ重要度はProbabilityで定義することができる：

すべての成分のBirnbaumImportance：

成分の信頼性の欠如を系の信頼性の欠如で割った成分の重み：

結果のクリティカリティ故障重要度：

定義と比較する：

故障に基づいたクリティカリティ重要度はRiskReductionImportanceと関係がある：

定義と比較する：

故障に基づいたクリティカリティ重要度はImprovementImportanceと関係がある：

ImprovementImportanceを計算する：

改善の重要度を系の信頼性の欠如で割る：

定義と比較する：

並列の系では，故障に基づいたクリティカリティ重要度はすべての成分について常に1である：

無関係の成分の重要度は0である：

Wolfram Research (2012), CriticalityFailureImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html.

テキスト

Wolfram Research (2012), CriticalityFailureImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html.

CMS

Wolfram Language. 2012. "CriticalityFailureImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html.

APA

Wolfram Language. (2012). CriticalityFailureImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html

BibTeX

@misc{reference.wolfram_2024_criticalityfailureimportance, author="Wolfram Research", title="{CriticalityFailureImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_criticalityfailureimportance, organization={Wolfram Research}, title={CriticalityFailureImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/CriticalityFailureImportance.html}, note=[Accessed: 22-November-2024 ]}