RiskAchievementImportance

RiskAchievementImportance[rdist,t]

gives the risk achievement importances for all components in the ReliabilityDistribution rdist at time t.

RiskAchievementImportance[fdist,t]

gives the risk achievement importances for all components in the FailureDistribution fdist at time t.

Details

  • RiskAchievementImportance is also known as risk achievement worth.
  • The risk achievement importance at time t for component 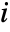is given by 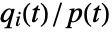, where 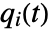is the probability that the system failed given that the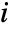 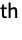^(th) component has failed, and 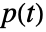is the probability that the system has failed.
  • The results are returned in the component order given in the distribution list in rdist or fdist.

Examples

open allclose all

Basic Examples  (3)

Two components connected in series, with different lifetime distributions:

The result is given in the same order as the distribution list in ReliabilityDistribution:

Two components connected in parallel, with different lifetime distributions:

Use fault tree-based modeling to define the system:

Scope  (19)

ReliabilityDistribution Models  (10)

Two components connected in parallel, with identical lifetime distributions:

The importance is identical:

Two components connected in series, with identical lifetime distributions:

The importance is identical:

A system where two out of three components need to work, with identical lifetime distributions:

The importance is identical:

A simple mixed system with identical lifetime distributions:

Compute the importance:

Component is most important, and and are equally important because of symmetry:

A system with a series connection in parallel with a component:

Show the importance:

Study the effect of a change in parameter in a simple mixed system:

Compute the importance:

Show the changes in importance when worsening one of the parallel components, :

One component in parallel with two others, with different distributions:

Find the importance measures at one specific point in time as exact results:

As machine-precision results:

As symbolic expressions:

Any valid ReliabilityDistribution can be used:

The more reliable component is more important:

ReliabilityDistribution can contain many different distributions:

Model the system in steps to get the importance measure for a subsystem:

Plot the importance over time:

FailureDistribution Models  (9)

Any of two basic events lead to the top event:

The importance is identical:

Only both basic events together lead to the top event:

The importance is identical:

A voting gate, with identical distributions on the basic events:

The importance is identical:

A simple system with both And and Or gates:

The basic event is most important:

A simple system with both And and Or gates:

Show the importance:

Study the effect of a change in parameter in a simple mixed system:

Compute the importance:

Show the changes in importance when worsening one of the basic events, :

Any valid FailureDistribution can be used:

The more reliable component is more important:

FailureDistribution can contain many different distributions:

Model the system in steps to get the importance measure for a subsystem:

Plot the importance over time:

Applications  (3)

Find out which component has the highest potential to make the system unreliable for a mission time of 1 day:

Show the importance over time:

With a mission time of 1 day, component could worsen the system reliability the most if it failed:

The importance measure is the factor with which the system unreliability can be increased by worsening . The worst case is a failed , which results in an unreliability of 1:

Analyze what component has the highest risk achievement importance for the launch of an aircraft. The hangar door can be opened electronically or manually:

Two fuel pumps require power to run:

Two more pumps run on reliable batteries, giving the following fuel transfer structure:

Also needed is deicing of the aircraft and a fuel storage tank:

Define the lifetime distributions:

Compute the importance:

The fuel storage should be monitored to avoid a high unreliability increase:

Consider a water pumping system, with one valve and two redundant pumps. The reliability of the components is given as probabilities:

The valve needs to be monitored and maintained most to avoid a high increase in unreliability:

Properties & Relations  (4)

RiskAchievementImportance can be defined in terms of Probability:

Compute the base reliability for the system:

The reliability for the system when the component is failed:

Divide the reliability with a failed component with the base reliability:

RiskAchievementImportance approaches 1 as :

The RiskAchievementImportance is the same for all components in a series system:

Irrelevant components have importance 1:

Wolfram Research (2012), RiskAchievementImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/RiskAchievementImportance.html.

Text

Wolfram Research (2012), RiskAchievementImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/RiskAchievementImportance.html.

CMS

Wolfram Language. 2012. "RiskAchievementImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RiskAchievementImportance.html.

APA

Wolfram Language. (2012). RiskAchievementImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiskAchievementImportance.html

BibTeX

@misc{reference.wolfram_2024_riskachievementimportance, author="Wolfram Research", title="{RiskAchievementImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/RiskAchievementImportance.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riskachievementimportance, organization={Wolfram Research}, title={RiskAchievementImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/RiskAchievementImportance.html}, note=[Accessed: 22-November-2024 ]}