FussellVeselyImportance

FussellVeselyImportance[rdist,t]

gives the Fussell–Vesely importances for all components in the ReliabilityDistribution rdist at time t.

FussellVeselyImportance[fdist,t]

gives the Fussell–Vesely importances for all components in the FailureDistribution fdist at time t.

Details

  • The Fussell–Vesely importance at time 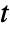for component 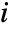is given by 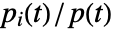where 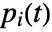is the probability that at least one minimal cut set containing component 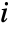has failed at time 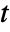and 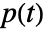is the probability that the system has failed at time 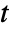. A minimal cut set is a minimal set of components which, if failed, causes the system to fail.
  • The results are returned in the component order given in the distribution list in rdist or fdist.

Examples

open allclose all

Basic Examples  (3)

Two components connected in series, with different lifetime distributions:

The result is given in the same order as the distribution list in ReliabilityDistribution:

Two components connected in parallel, with different lifetime distributions:

Use fault tree-based modeling to define the system:

Scope  (16)

ReliabilityDistribution Models  (8)

Two components connected in series, with identical lifetime distributions:

A change in reliability for either component will result in the same system reliability change:

A system where two out of three components need to work, with identical lifetime distributions:

Components are equally important:

A simple mixed system with identical lifetime distributions:

Compute the importance:

Changing the reliability of component x will impact the system reliability most:

A system with a series connection in parallel with a component:

Compute the importance:

Improving the x component has the biggest impact on system reliability:

Study the effect of a change in parameter in a simple mixed system:

Compute the importance:

Show the changes in importance when worsening one of the parallel components, z:

One component in parallel with two others, with different distributions:

Find the importance measures at one specific point in time as exact results:

As machine precision results:

As symbolic expressions:

Any valid ReliabilityDistribution can be used:

Later in the lifetime, changing the reliability of the standby component y will have more effect:

Model the system in steps to get the importance measure for a subsystem:

Plot the importance over time:

FailureDistribution Models  (8)

Either of two basic events lead to the top event:

A change in reliability for either event will result in the same top event reliability change:

Only both basic events together lead to the top event:

FussellVeselyImportance will rank both events as equally important:

A voting gate with identical distributions on the basic events:

A change in reliability for any of the events will result in the same top event reliability change:

A simple system with both And and Or gates:

The basic event x is most important:

Changing the reliability of event x will impact the top event reliability most:

A simple system with both And and Or gates:

Compute the importance:

Improving event x has the biggest impact on preventing the top event:

Study the effect of a change in parameter in a simple mixed system:

Compute the importance:

Show the changes in importance when worsening one of the basic events, z:

Any valid FailureDistribution can be used:

Early in the lifetime, changing the reliability of the standby component y will have more effect:

Model the system in steps to get the importance measure for a subsystem:

Plot the importance over time:

Applications  (3)

Find out which component is most important in a system that has to last for three hours:

Component v is most important according to the Fussell–Vesely importance:

A problem at coal mines is bulldozers falling through bridged voids in coal piles. The bulldozer can be over a void intentionally or unintentionally:

To form a void, there has to be subsurface flow in the coal. This requires removal of coal from below on a conveyor belt, and an open feeder to that belt:

It is also required that no flow occurs on the surface. This can happen if the coal freezes:

Compacted coal can also lead to a non-flowing surface:

The complete fault tree:

Assume the following distributions for the events:

To determine what actions to take to avoid accidents, compute the importance of the basic events:

We can see that the events with importance 1 are the highest:

Find the basic events with importance 1:

Consider a water pumping system with one valve and two redundant pumps. The reliability of the components are given as probabilities:

Find out which components are most important:

Properties & Relations  (6)

FussellVeselyImportance for serial connections can be defined in terms of probability:

All parallel systems have FussellVeselyImportance equal to 1:

Subsystems with parallel structure will have the same importance:

CriticalityFailureImportance is always less than or equal to Fussell–Vesely importance:

CriticalityFailureImportance approaches Fussell–Vesely for highly reliable components:

Compute the difference:

The difference is always when the failure rate approaches :

Irrelevant components have importance 0:

Wolfram Research (2012), FussellVeselyImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/FussellVeselyImportance.html.

Text

Wolfram Research (2012), FussellVeselyImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/FussellVeselyImportance.html.

CMS

Wolfram Language. 2012. "FussellVeselyImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FussellVeselyImportance.html.

APA

Wolfram Language. (2012). FussellVeselyImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FussellVeselyImportance.html

BibTeX

@misc{reference.wolfram_2024_fussellveselyimportance, author="Wolfram Research", title="{FussellVeselyImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FussellVeselyImportance.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fussellveselyimportance, organization={Wolfram Research}, title={FussellVeselyImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/FussellVeselyImportance.html}, note=[Accessed: 22-December-2024 ]}