CyclicGroup

CyclicGroup[n]

次数 n の巡回群である．

詳細

  • CyclicGroup[n]の次数 n は，非負の整数でなければならない．次数0および1は，自明群か恒等群に対応する．
  • CyclicGroup[n]はデフォルトで点{1,…,n}の置換群として表される．
  • 巡回群は可換である．

予備知識

  • CyclicGroup[n]は，与えられた非負の整数 n についての n 次巡回群 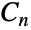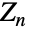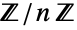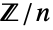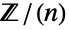（，，，と表示されることもあり）を表す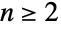．のとき，CyclicGroup[n]のデフォルト表現はシンボルの置換群としてである．特殊なケースのCyclicGroup[0]およびCyclicGroup[1]は元の数が厳密に1つの自明群に等しい．
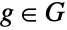  • 数学的には，巡回群は生成元として知られる元 を含む群 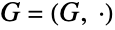であり，すべての元 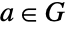を 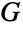の位数より小さい非負の整数 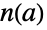について 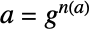の形で書くことができる．すべての元 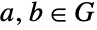について 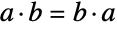なので，このような 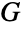はすべてアーベル群（つまり可換群）である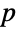． が素数のとき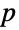， 個の元を持つ任意の群はCyclicGroup[p]と同型であり，有限アーベル群の基本定理により，有限個の元を持つすべてのアーベル群 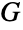は直積 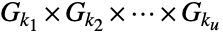として表すことができる．ただし，Gki=CyclicGroup[ki]であり，各 kiは素数のベキ乗である．巡回群は置換群である．
  • CyclicGroup[n]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．巡回群 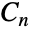の数多くの計算済み特性をFiniteGroupData[{"CyclicGroup",n},"prop"]によって得ることができる．
  • 巡回群のクラスは，実質的巡回群，局所巡回群，多環群を含む関連する多くの一般化の基礎となっている．これらの多くが抽象代数学，整数論，幾何学的群論，位相幾何学において根本的な重要性を有している．
  • Wolfram言語に組み込まれた，整数でパラメータ化される他の有限群の無限族には，AbelianGroup，AlternatingGroup，DihedralGroup，SymmetricGroupがある．

例題

すべて開くすべて閉じる

例  (3)

巡回群の元の数：

巡回群の置換の生成元：

巡回群の置換表現の元：

スコープ  (1)

次数が0または1である巡回群は，自明群であり，単位元のみを含む：

その他の場合，次数 n の巡回群は，n 個の要素を含む：

特性と関係  (1)

次数 n の巡回群は，整数{0,…,n-1}と n を法とする数の加算を使って表すことができる：

Wolfram Research (2010), CyclicGroup, Wolfram言語関数， https://reference.wolfram.com/language/ref/CyclicGroup.html.

テキスト

Wolfram Research (2010), CyclicGroup, Wolfram言語関数， https://reference.wolfram.com/language/ref/CyclicGroup.html.

CMS

Wolfram Language. 2010. "CyclicGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CyclicGroup.html.

APA

Wolfram Language. (2010). CyclicGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CyclicGroup.html

BibTeX

@misc{reference.wolfram_2024_cyclicgroup, author="Wolfram Research", title="{CyclicGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CyclicGroup.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cyclicgroup, organization={Wolfram Research}, title={CyclicGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/CyclicGroup.html}, note=[Accessed: 22-November-2024 ]}