WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

DihedralGroup

DihedralGroup[n]

次数 2n の二面体群である．

詳細

DihedralGroup[n]の次数 n は，正の整数でなければならない．
DihedralGroup[1]はCyclicGroup[2]の同型群であり，デフォルトで点{1,2}上の置換群として表される．
DihedralGroup[2]はAbelianGroup[{2,2}]の同型群であり，デフォルトで点{1,2,3,4}上の置換群として表される．
n≥3の場合，DihedralGroup[n]はデフォルトで点{1,…,n}上の置換群として表される．

予備知識

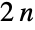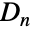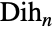DihedralGroup[n]は，指定された正の整数 n についての，位数がの二面体群を表す（あるいは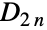と表記されることもある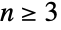）．のとき，DihedralGroup[n]のデフォルト表現はシンボル上の置換表現である．特殊ケースのDihedralGroup[1]およびDihedralGroup[2]は，順にCyclicGroup[2]およびAbelianGroup[{2,2}]と同型であり，デフォルトで，順にシンボル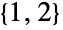および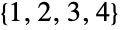上の置換群として表される．
二面体群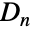は，数学的には，正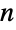角形の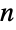通りの回転と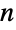通りの鏡映である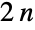個の対称変換からなる．特に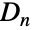，は（回転）と（鏡映）の元からなる．これらを組み合せるとその群作用下で恒等式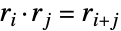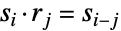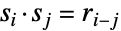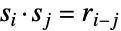，，，に従って変換が行われる．ただし，加減演算は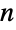を法として行われる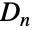．は置換群であるが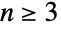，では鏡映と回転の操作が一般に可換ではなくなる，つまり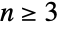，のとき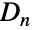は非可換である．
二面体群は，対称性を有する化合物や結晶学の特性決定を含む，正規構造の分析において重要である．
DiherdalGroup[n]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．二面体群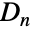の数多くの計算済みの特性を，FiniteGroupData[{"DihedralGroup",n},"prop"]を介して得ることができる．
DihedralGroupは他の数多くのシンボルに関連している．DihedralGroup[n]はCyclicGroup[n]とCyclicGroup[2]の半直積（反転によって後者が前者に対して作用する）と同型であり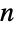，が偶数のとき，DihedralGroup[n]はDihedralGroup[n/2]とCyclicGroup[2]の直積と同型である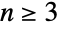．のとき，二面体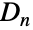群は対称群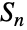の部分群である．Wolfram言語に組み込まれた他の有限群の無限族にAbelianGroup，AlternatingGroup，CyclicGroup，SymmetricGroupがある．

例題

すべて開くすべて閉じる

例 (3)

二面体群の元の数：

二面体群の置換の生成元：

二面体群の置換表現の元：

スコープ (1)

任意の正の整数 n のDihedralGroup[n]：

特性と関係 (1)

DihedralGroup[1]とDihedralGroup[2]は，唯一の二面体可換群である：

考えられる問題 (1)

DihedralGroup[1]とDihedralGroup[2]は，それぞれ SymmetricGroup[1]とSymmetricGroup[2]の部分群ではないので，置換群としては特別である．この2つの置換表現にはより大きな台が必要である：

トップへ