DihedralGroup
表示阶数为 2n 的二面体群.
更多信息
- DihedralGroup[n] 的度数 n 必须是一个正整数.
- DihedralGroup[1] 与 CyclicGroup[2] 同构,并且默认情况下,表示为点 {1,2} 上的一个置换群.
- DihedralGroup[2] 与 AbelianGroup[{2,2}] 同构,并且默认情况下,表示为点 {1,2,3,4} 上的一个置换群.
- 对于 n≥3,DihedralGroup[n] 默认情况下表示为点 {1,…,n} 上的一个置换群.
背景
- DihedralGroup[n] 表示阶为
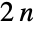 的二面体群
的二面体群 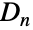 (也表示为
(也表示为 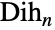 或
或 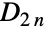 ),其中 n 为已知正整数. 对于
),其中 n 为已知正整数. 对于 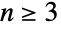 ,DihedralGroup[n] 的默认表示是符号
,DihedralGroup[n] 的默认表示是符号  上的置换群. 特殊情形 DihedralGroup[1] 和 DihedralGroup[2] 分别与 CyclicGroup[2] 和 AbelianGroup[{2,2}] 同构,并分别默认表示为符号
上的置换群. 特殊情形 DihedralGroup[1] 和 DihedralGroup[2] 分别与 CyclicGroup[2] 和 AbelianGroup[{2,2}] 同构,并分别默认表示为符号 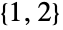 和
和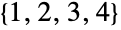 上的置换群.
上的置换群. - 数学上说,二面体群
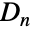 由正
由正 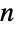 边形的
边形的 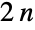 个对称组成,即
个对称组成,即 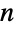 个旋转对称和
个旋转对称和 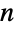 个反射对称. 特别地,
个反射对称. 特别地,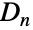 由元素
由元素  (旋转)和
(旋转)和  (对称),根据恒等式
(对称),根据恒等式 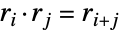 、
、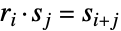 、
、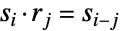 和
和 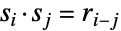 组合在其群操作下转换,其中执行加法和减法模除
组合在其群操作下转换,其中执行加法和减法模除 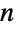 .
. 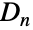 是置换群,但对于
是置换群,但对于 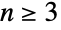 ,反射和旋转运算一般会失败,这意味着对于
,反射和旋转运算一般会失败,这意味着对于 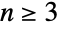 ,
,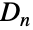 是非阿贝尔群.
是非阿贝尔群. - 二面体群在常规结构分析中很重要,包括在对称化合物的性质和晶体学的测定中.
- 通常的群论函数可以应用于 DiherdalGroup[n],包括 GroupOrder、GroupGenerators 和 GroupElements 等等. 二面体群
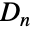 的若干预计算属性通过 FiniteGroupData[{"DihedralGroup",n},"prop"] 可用.
的若干预计算属性通过 FiniteGroupData[{"DihedralGroup",n},"prop"] 可用. - DihedralGroup 与很多其它符号相关. DihedralGroup[n] 与 CyclicGroup[n] 和 CyclicGroup[2] 半直接乘积同构(其中后者通过倒置作用在前者上),并且对于偶数
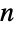 ,DihedralGroup[n] 与 DihedralGroup[n/2] 和CyclicGroup[2] 的直接乘积同构. 对于
,DihedralGroup[n] 与 DihedralGroup[n/2] 和CyclicGroup[2] 的直接乘积同构. 对于 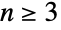 ,二面体群
,二面体群 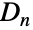 是对称群
是对称群 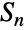 的子群. 通过整数参数化的 Wolfram 语言内置有限群的其它无限族包括 AbelianGroup、 AlternatingGroup、CyclicGroup 和 SymmetricGroup.
的子群. 通过整数参数化的 Wolfram 语言内置有限群的其它无限族包括 AbelianGroup、 AlternatingGroup、CyclicGroup 和 SymmetricGroup.
范例
打开所有单元关闭所有单元范围 (1)
对于任意正整数 n,DihedralGroup[n]:
属性和关系 (1)
DihedralGroup[1] 和 DihedralGroup[2] 是唯一的二面体交换群:
可能存在的问题 (1)
DihedralGroup[1] 和 DihedralGroup[2] 作为置换群是特殊的,因为它们并不分别是 SymmetricGroup[1] 和 SymmetricGroup[2] 的子群. 它们的置换表示要求用更大的支集:
Wolfram Research (2010),DihedralGroup,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DihedralGroup.html.
文本
Wolfram Research (2010),DihedralGroup,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DihedralGroup.html.
CMS
Wolfram 语言. 2010. "DihedralGroup." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DihedralGroup.html.
APA
Wolfram 语言. (2010). DihedralGroup. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DihedralGroup.html 年