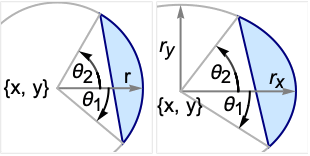
DiskSegment
DiskSegment[{x,y},r,{θ1,θ2}]
represents the disk segment from angle θ1 to θ2 in a disk centered at {x,y} of radius r.
DiskSegment[{x,y},{rx,ry},{θ1,θ2}]
represents the ellipse segment from angle θ1 to θ2 in an axis-aligned ellipse with semiaxes lengths rx and ry.
Details and Options

- DiskSegment can be used as a geometric region and a graphics primitive.
- DiskSegment represents the filled segment part of Disk with the same arguments.
- Angles are measured in radians counterclockwise from the positive x direction.
- DiskSegment can be used in Graphics.
- In graphics, the point {x,y} can be Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, and color.
Examples
open allclose allBasic Examples (5)
A segment of an elliptical disk:
Differently styled disk segments:
Get the Area of a disk segment (half disk):
Scope (17)
Graphics (7)
Styling (2)
Coordinates (1)
Points can be Dynamic:
Applications (5)
Plot a function over a disk segment:
Create a 3D disk segment extrusion with RegionProduct:
To show the region difference between a disk and a regular polygon, a set of disk segments may be used. First you get a set of arcs:
However, some of arcs are not increasing angle ranges, so in those cases ![]() is added to the second angle to make it increasing:
is added to the second angle to make it increasing:
A lens can be modeled as two adjacent disk segments. Create a rightward-facing lens segment of height ![]() and radius of
and radius of ![]() , centered on the origin:
, centered on the origin:
For the leftward-facing part of the lens, you need to switch the ![]() position and switch the direction of the arc:
position and switch the direction of the arc:
Now make a function that will construct a pair of disk segments for given height and radii, and visualize it for a range of radius values:
You can find an approximate measure of a region by finding the fraction of random points within a region of known volume that fall within the region whose measure you seek. Use a disk segment as an example:
This region can be contained within the region ![]() and
and ![]() , which has an area of 16. Generate a list of random points within this general region:
, which has an area of 16. Generate a list of random points within this general region:
Find the percent of these random points that fall within the disk segment:
The area of the region (the disk segment) should be close to that ratio times the area over which the random points are distributed. Compare this approximation to the actual value:
Properties & Relations (4)
DiskSegment can be represented by a FilledCurve:
A disk segment may result from the RegionIntersection of a Disk and another region:
ImplicitRegion can represent any DiskSegment:
ParametricRegion can represent a DiskSegment:
Text
Wolfram Research (2015), DiskSegment, Wolfram Language function, https://reference.wolfram.com/language/ref/DiskSegment.html.
CMS
Wolfram Language. 2015. "DiskSegment." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiskSegment.html.
APA
Wolfram Language. (2015). DiskSegment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiskSegment.html