SphericalShell
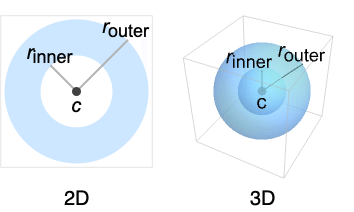
SphericalShell[c,{rinner,router}]
represents a filled spherical shell centered at c with inner radius rinner and outer radius router.
Details and Options
- SphericalShell can be used as a geometric region and a graphics primitive.
- SphericalShell[] is equivalent to SphericalShell[{0,0,0},{1/2,1}].
- SphericalShell[r] is equivalent to SphericalShell[{0,0,0},{r/2,r}].
- SphericalShell[{rinner,router}] is equivalent to SphericalShell[{0,0,0},{rinner,router}].
- SphericalShell represents a filled spherical shell
![{x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)}](Files/SphericalShell.en/2.png "{x|r_(inner)<=TemplateBox[{{x, -, c}}, Norm]<=r_(outer)}")
. The region is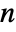 
dimensional for point c of length 
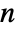. - SphericalShell allows c to be any point in
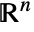and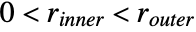 
. - SphericalShell can be used in Graphics and Graphics3D.
- In graphics, the point c and radius r can be Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Specularity, Opacity, and color.
Examples
open allclose allScope (20)
Graphics (10)
Regions (10)
Embedding dimension is the dimension of the space in which the spherical shell lives:
Geometric dimension is the dimension of the shape itself:
Get conditions for point membership:
The equidistance contours for a spherical shell:
Nearest points to an enclosing sphere:
Integrate over a spherical shell region:
Applications (5)
A standard Ping-Pong ball, a spherical shell, has a mass of 2.7 grams and an outer radius of 40 millimeters:
It is made of celluloid, which has a density of 
. Knowing that 
, find the inner radius of a Ping-Pong ball:
The thickness is the difference between the inner and outer radius:
It was once believed that the universe was a system of concentric celestial spheres. At the center of the universe was Earth, and surrounding it were the spherical shells for the planets and the Sun. There was disagreement about the exact order of the planets and the Sun. Plato and Ptolemy ordered the celestial spheres differently:
Visualize and compare the two philosophers' universes using a set of labeled spherical shells:
A pearl is formed, layer by layer, by a mollusk. The pearl's optical properties come from light reflecting off many translucent layers, as opposed to only an opaque surface layer. The difference that translucent layers make can be seen by creating two sets of nested spherical shells that differ in opacity:
Golf balls have multiple layers, the outer, dimpled shell, and one or more inner layers. Model the outer layer as the RegionDifference between a spherical shell and a collection of balls. Get a distribution for the dimples using the MeshCoordinates of a sphere's mesh:
Discretize the region over an interval to get a "cut-away" view of half of it:
Finally, make a ball for the inner core of the golf ball, offset from the center to get a visual separation of layers:
A balloon can be approximated as a spherical shell. Suppose the balloon is made of 10 units of material. Find out how the thickness depends on the outer radius of the balloon:
Suppose the material is such that under the given conditions it will break if it has thickness less than 
. Find the largest possible outer radius balloon given that constraint:
Properties & Relations (4)
A Ball is the limit of SphericalShell as 
approaches 0:
A Sphere is the limit of SphericalShell as 
goes to 
:
A SphericalShell is the closure of RegionDifference between two concentric Ball regions:
SphericalShell is all points less than 
from a sphere of radius 
:
Text
Wolfram Research (2015), SphericalShell, Wolfram Language function, https://reference.wolfram.com/language/ref/SphericalShell.html.
CMS
Wolfram Language. 2015. "SphericalShell." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SphericalShell.html.
APA
Wolfram Language. (2015). SphericalShell. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SphericalShell.html