WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

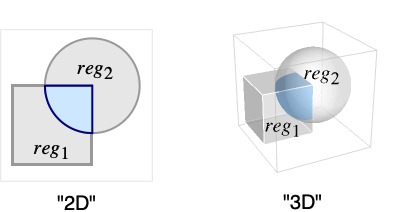
RegionIntersection
✖
RegionIntersection

✖
RegionIntersection[reg1,reg2,…]

gives the intersection of the regions reg1, reg2, ….

Details and Options

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Intersection of two disks:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-bwhjpw

Visualize it:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-kgyvnb
Out[2]=2

Intersection of two MeshRegion objects:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-i47t61
Out[1]=1

Scope  (13)Survey of the scope of standard use cases

Special Regions  (7)

For some regions, intersection is computed explicitly:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-d1ggqp
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-1bowl
Out[3]=3

Visualize the intersection:

In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-bmt7by
Out[4]=4

An intersection of an infinite line and a ball:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-dsd1ix
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-bxmu06
Out[2]=2

Visualize the intersection:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-bq9s2l
Out[3]=3

An intersection of Line regions:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-cl5o55
Out[1]=1

Visualize it:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-kq6iqq
Out[2]=2

An intersection of Polygon regions:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-h9631g
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-i01vvp

Visualize it:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-unxw
Out[3]=3

An intersection of two Disk regions:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-hl5gpm

Visualize it:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-eewuc0
Out[2]=2

An intersection of a cuboid a cone:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-59fdh

Visualize it:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-v9k9l6
Out[2]=2

An intersection of regions with different RegionDimension:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-dq7yx6
Out[1]=1

Visualize it:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-of250
Out[2]=2

Formula Regions  (2)

An intersection of ImplicitRegion objects is an ImplicitRegion:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-crtuk1
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-i34nki
Out[3]=3

2D:

In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-gc5987
In[6]:=6
✖
https://wolfram.com/xid/0g7ijzrxagi-bqytv
Out[6]=6

3D:

In[7]:=7
✖
https://wolfram.com/xid/0g7ijzrxagi-daco4v
In[9]:=9
✖
https://wolfram.com/xid/0g7ijzrxagi-sa2or
Out[9]=9

nD:

In[10]:=10
✖
https://wolfram.com/xid/0g7ijzrxagi-bdn04e
In[12]:=12
✖
https://wolfram.com/xid/0g7ijzrxagi-iw2h19
Out[12]=12

An intersection of ParametricRegion objects:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-d62uqc
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-d7q2hj

Visualize it:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-hh12
Out[3]=3

Mesh Regions  (2)

An intersection of BoundaryMeshRegion objects is a BoundaryMeshRegion:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-k2if8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-ehdu8m
Out[3]=3

2D:

In[6]:=6
✖
https://wolfram.com/xid/0g7ijzrxagi-d1hr7s
Out[6]=6
In[8]:=8
✖
https://wolfram.com/xid/0g7ijzrxagi-4rlzu
Out[8]=8

3D:

In[9]:=9
✖
https://wolfram.com/xid/0g7ijzrxagi-e0i5c3
Out[9]=9
In[12]:=12
✖
https://wolfram.com/xid/0g7ijzrxagi-co8192
Out[12]=12

An intersection of full-dimensional MeshRegion objects is a MeshRegion:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-bnl5n5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-cadjtl
Out[2]=2

2D:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-b2vn5v
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-b5oxqo
Out[4]=4

3D:

In[5]:=5
✖
https://wolfram.com/xid/0g7ijzrxagi-im6jks
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0g7ijzrxagi-qu8qa
Out[6]=6

Derived Regions  (2)

An intersection of BooleanRegion objects:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-fzcaz8
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-i5hp5n

Visualize it:

In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-b3gvca
Out[4]=4

An intersection of TransformedRegion objects:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-fdpyhr
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-dp6ddh

Visualize it:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-c2ee5
Out[3]=3

Applications  (3)Sample problems that can be solved with this function

Intersection of regions:

In[5]:=5
✖
https://wolfram.com/xid/0g7ijzrxagi-ysokjf
In[6]:=6
✖
https://wolfram.com/xid/0g7ijzrxagi-7tcgzk
Out[6]=6

Define a disk segment as an intersection of a disk and a half-plane:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-ndz2ni
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-pqnqkk
Out[2]=2

Define a new basic region diskSegment that uses the same notation as Disk does for disk sectors, so that diskSegment[{x,y},r,{θ1,θ2}] represents the disk segment from θ1 to θ2. Do it by writing it as a RegionIntersection of a Disk and a HalfPlane:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-8t48i

This evaluates an object that is RegionQ and can be used as any other region:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-o87dci
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-fjl35
Out[3]=3

Visualize the disk segment together with the disk:

In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-52yn5u
Out[4]=4

Properties & Relations  (4)Properties of the function, and connections to other functions

A point p belongs to RegionIntersection[reg1,reg2,…] if it belongs to all regi:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-c2sfwz

Use RegionMember to test membership:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-i0bat4
In[12]:=12
✖
https://wolfram.com/xid/0g7ijzrxagi-gq7lk1
Out[12]=12

RegionIntersection is a Boolean combination And of regions:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-fgv0t7
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-ehtogm
Out[2]=2

The RegionMeasure of an intersection obeys a simple formula:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-hjvs0m

Subtract the measure of the RegionUnion from the sum of the measures:

In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-f0wukb
Out[2]=2

The RegionDimension of an intersection is at most the minimum of all input dimensions:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-qehjx
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-ljzl3
Out[2]=2

It can be lower, however:

In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-eww4bw
In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-dgrigy
Out[4]=4

These regions overlap only at a point, so the dimension of the intersection is 0:

In[5]:=5
✖
https://wolfram.com/xid/0g7ijzrxagi-mgykir
Out[5]=5

Possible Issues  (2)Common pitfalls and unexpected behavior

RegionIntersection is defined only for regions with the same RegionEmbeddingDimension:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-dqoj2
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-hnwr2q
Out[3]=3

Components of dimension less than the embedding dimension may be omitted:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-p6rhkn
In[2]:=2
✖
https://wolfram.com/xid/0g7ijzrxagi-s5yjch
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0g7ijzrxagi-n45d6y
Out[3]=3

Turn on a message:

In[4]:=4
✖
https://wolfram.com/xid/0g7ijzrxagi-oqb0ib
In[5]:=5
✖
https://wolfram.com/xid/0g7ijzrxagi-7gcaf2
Out[5]=5

Neat Examples  (1)Surprising or curious use cases

The intersection of two spiral polygons:

In[1]:=1
✖
https://wolfram.com/xid/0g7ijzrxagi-bv5wci
Out[1]=1
Wolfram Research (2014), RegionIntersection, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionIntersection.html (updated 2017).
✖
Wolfram Research (2014), RegionIntersection, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionIntersection.html (updated 2017).

Text

Wolfram Research (2014), RegionIntersection, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionIntersection.html (updated 2017).

✖
Wolfram Research (2014), RegionIntersection, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionIntersection.html (updated 2017).

CMS

Wolfram Language. 2014. "RegionIntersection." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RegionIntersection.html.

✖
Wolfram Language. 2014. "RegionIntersection." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RegionIntersection.html.

APA

Wolfram Language. (2014). RegionIntersection. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionIntersection.html

✖
Wolfram Language. (2014). RegionIntersection. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionIntersection.html

BibTeX

@misc{reference.wolfram_2025_regionintersection, author="Wolfram Research", title="{RegionIntersection}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionIntersection.html}", note=[Accessed: 04-June-2025 ]}

✖
@misc{reference.wolfram_2025_regionintersection, author="Wolfram Research", title="{RegionIntersection}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionIntersection.html}", note=[Accessed: 04-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_regionintersection, organization={Wolfram Research}, title={RegionIntersection}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionIntersection.html}, note=[Accessed: 04-June-2025 ]}

✖
@online{reference.wolfram_2025_regionintersection, organization={Wolfram Research}, title={RegionIntersection}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionIntersection.html}, note=[Accessed: 04-June-2025 ]}