DiskSegment

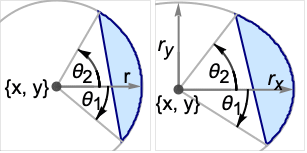
DiskSegment[{x,y},r,{θ1,θ2}]

{x,y}を中心とした半径 r の円板の，角度 θ1から θ2までの部分を表す．

DiskSegment[{x,y},{rx,ry},{θ1,θ2}]

半軸の長さが rxと ryで軸に平行な楕円の，角度 θ1から θ2までの部分を表す．

詳細とオプション

  • DiskSegmentは，幾何学領域およびグラフィックスプリミティブとして使うことができる．
  • DiskSegmentは，同じ引数を持つDiskの塗り潰された部分を表す．
  • 角度は，正の x 方向からラジアン単位で反時計回りに測られる．
  • DiskSegmentはGraphicsで使うことができる．
  • グラフィックスでは，点{x,y}はDynamic式でよい．
  • グラフィックスの描画は，FaceForm，EdgeForm等の指示子および色の影響を受ける．

例題

すべて開くすべて閉じる

例  (5)

単位円板の半分：

円板の一部：

楕円板の一部：

さまざまにスタイル付けされた円板の一部：

円板の一部（半円板）のAreaを得る：

楕円板の一部の面積：

スコープ  (17)

グラフィックス  (7)

指定  (4)

半径を指定する：

中心を指定する：

角度を指定する：

楕円板の一部：

スタイル付け  (2)

色指示子で円板の一部の表面の色を指定する：

FaceFormとEdgeFormを使って内側と境界のスタイルを指定することができる：

円板の一部の境界：

座標  (1)

点はDynamicでよい：

領域  (10)

埋込み次元：

幾何次元：

点の帰属判定：

点の帰属条件を得る：

面積：

重心：

点からの距離：

点からの符号付き距離：

領域内の最近点：

最近点：

楕円の一部は有界である：

その領域を得る：

楕円の一部の上で積分する：

楕円の一部の上で最適化する：

楕円の一部の上で方程式を解く：

アプリケーション  (5)

円板の一部の上で関数をプロットする：

RegionProductで3Dの円板の一部の押出し形成を作る：

円板と正多角形の領域の差を示すために，部分円板の集合を使うことができる．まず，弧の集合を得る：

しかし，弧の中には角が大きくならないものもある．そのような場合は 2番目の弧に を加えて増加するようにする：

最後にこれを可視化する：

レンズは隣接する2つの弧の部分としてモデル化することができる．原点を中心とする，高さ，半径 の右側に膨らむレンズを作る：

左側に膨らむレンズは， の位置を入れ替えて，弧の向きを変える必要がある：

指定された高さと半径の円板のペアを作る関数を構築し，半径の範囲で可視化する：

求める測度の領域内にある既知の体積範囲のランダムな点との割合として領域の近似測度を求めることができる．部分円板を例として使う：

この領域は，面積が16の領域および内にあるの．この一般的な領域内にあるランダムな点のリストを生成する：

部分円板内にあるこのランダムな点の割合を百分率で求める：

この領域（部分円板）の面積は上記の割合に点が分布している面積をかけたものに近いはずである．ここで得られた近似値を実際の値と比較する：

特性と関係  (4)

DiskSegmentはFilledCurveによって表すことができる：

円板の一部はDiskやその他の領域のRegionIntersectionの結果であることがある：

ImplicitRegionは任意のDiskSegmentを表すことができる：

ParametricRegionはDiskSegmentを表すことができる：

おもしろい例題  (3)

ランダムな円板の一部の集合：

円板の一部の族：

デジタル花弁：

Wolfram Research (2015), DiskSegment, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiskSegment.html.

テキスト

Wolfram Research (2015), DiskSegment, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiskSegment.html.

CMS

Wolfram Language. 2015. "DiskSegment." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiskSegment.html.

APA

Wolfram Language. (2015). DiskSegment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiskSegment.html

BibTeX

@misc{reference.wolfram_2024_disksegment, author="Wolfram Research", title="{DiskSegment}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DiskSegment.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_disksegment, organization={Wolfram Research}, title={DiskSegment}, year={2015}, url={https://reference.wolfram.com/language/ref/DiskSegment.html}, note=[Accessed: 05-November-2024 ]}