EllipticLog

EllipticLog[{x,y},{a,b}]

楕円曲線 に関する一般化された対数を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • EllipticLog[{x,y},{a,b}]は，積分 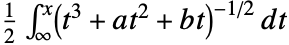の値として指定される．ただし，平方根の符号は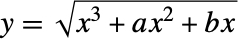， のような y の値により与えられる．
  • EllipticLogは任意の数値精度で評価できる．

例題

すべて開くすべて閉じる

例  (2)

数値的に評価する：

実数の部分集合上でプロットする：

スコープ  (16)

数値評価  (4)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

特定の値  (3)

固定点における値：

ゼロにおける値：

Abs[EllipticLog[{x,Sqrt[x^3+5x^2+x]},{5,1}]]=0.8となるような の値を求める：

可視化  (2)

EllipticLog関数をプロットする：

EllipticLog[{z,Sqrt[z^3+2 z^2+ z]},{2,1}]]の実部をプロットする：

EllipticLog[{x+ y,Sqrt[z^3+2 z^2+ z]},{2,1}]]の虚部をプロットする：

関数の特性  (3)

EllipticLogは解析関数ではない：

特異点と不連続点の両方を持つ：

は非負でも非正でもない：

は凸でも凹でもない：

微分  (2)

についての一次導関数：

Integrateを使って不定積分を計算する：

不定積分を確かめる：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

アプリケーション  (2)

楕円曲線 上で乗算を定義する：

楕円曲線上の乗算を使って有理数を加算する：

乗算の点におけるEllipticLogの値は対応する因数におけるEllipticLogの値の和と一致する：

EllipticLogをCarlsonRFで表す：

特性と関係  (3)

微分：

EllipticExpとEllipticLogは互いに逆関数である：

EllipticLogはInverseWeierstrassP関数と密接な関係がある：

数値的に評価する：

組込み関数の値と比較する：

Wolfram Research (1988), EllipticLog, Wolfram言語関数， https://reference.wolfram.com/language/ref/EllipticLog.html.

テキスト

Wolfram Research (1988), EllipticLog, Wolfram言語関数， https://reference.wolfram.com/language/ref/EllipticLog.html.

CMS

Wolfram Language. 1988. "EllipticLog." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticLog.html.

APA

Wolfram Language. (1988). EllipticLog. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticLog.html

BibTeX

@misc{reference.wolfram_2024_ellipticlog, author="Wolfram Research", title="{EllipticLog}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticLog.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ellipticlog, organization={Wolfram Research}, title={EllipticLog}, year={1988}, url={https://reference.wolfram.com/language/ref/EllipticLog.html}, note=[Accessed: 22-November-2024 ]}