InverseWeierstrassP

InverseWeierstrassP[p,{g2,g3}]

gives a value of u for which the Weierstrass function is equal to p.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The value of u returned always lies in the fundamental period parallelogram defined by the complex half‐periods 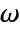and .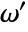
  • InverseWeierstrassP[{p,q},{g2,g3}] finds the unique value of u for which 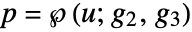and 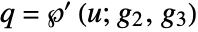. For such a value to exist, p and q must be related by .
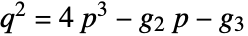  • InverseWeierstrassP can be evaluated to arbitrary numerical precision.

Examples

open allclose all

Basic Examples  (4)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Scope  (20)

Numerical Evaluation  (4)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number input:

Evaluate efficiently at high precision:

Specific Values  (4)

Values at fixed points:

Value at zero:

Find a value of x for which InverseWeierstrassP[x,{1,2}]=2:

TraditionalForm formatting:

Visualization  (2)

Plot the InverseWeierstrassP function for various parameters:

Plot the real part of TemplateBox[{z, 7, 1}, InverseWeierstrassP]:

Plot the imaginary part of TemplateBox[{z, 7, 1}, InverseWeierstrassP]:

Function Properties  (4)

InverseWeierstrassP has both singularities and discontinuities:

TemplateBox[{x, 1, 2}, InverseWeierstrassP] is injective:

TemplateBox[{x, 1, 2}, InverseWeierstrassP] is neither non-negative nor non-positive:

It is complex-valued over part of the real axis

TemplateBox[{x, {1, /, 2}, {1, /, 2}}, InverseWeierstrassP] is neither convex nor concave:

It is complex-valued over part of the real axis:

Differentiation  (2)

First derivative with respect to :

Higher derivatives with respect to :

Plot the higher derivatives with respect to when and :

Integration  (2)

Compute the indefinite integral using Integrate:

Verify the antiderivative:

Definite integral:

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Taylor expansion at a generic point:

Generalizations & Extensions  (1)

Evaluate the generalized form numerically:

These are the inverse relationships with WeierstrassP and WeierstrassPPrime:

Applications  (2)

Plot the real and imaginary part of InverseWeierstrassP:

Form derivatives:

Properties & Relations  (1)

InverseWeierstrassP is closely related to EllipticLog function:

Evaluate numerically:

Compare with the value of the built-in function:

Possible Issues  (2)

If the first argument does not represent a pair of values of Weierstrass functions, InverseWeierstrassP stays unevaluated:

InverseWeierstrassP evaluates to a vector‐valued first argument:

Wolfram Research (1996), InverseWeierstrassP, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

Text

Wolfram Research (1996), InverseWeierstrassP, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

CMS

Wolfram Language. 1996. "InverseWeierstrassP." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

APA

Wolfram Language. (1996). InverseWeierstrassP. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseWeierstrassP.html

BibTeX

@misc{reference.wolfram_2024_inverseweierstrassp, author="Wolfram Research", title="{InverseWeierstrassP}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverseweierstrassp, organization={Wolfram Research}, title={InverseWeierstrassP}, year={1996}, url={https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}, note=[Accessed: 22-December-2024 ]}