EstimatedDistribution
EstimatedDistribution[data,dist]
data からのパラメトリック分布 dist を推定する.
EstimatedDistribution[data,dist,{{p,p0},{q,q0},…}]
初期値を p0, q0, …として,母数 p, q, …を推定する.
EstimatedDistribution[data,dist,idist]
初期値を例示された分布 idist から取った分布 dist を推定する.
詳細とオプション

- EstimatedDistributionは,母数推定を任意の非数値のために挿入した分布 dist を返す.
- data は与えられた分布 dist からの可能な結果のリストでなければならない.
- 分布 dist は,母数が不明な任意の一変量あるいは多変量のパラメトリック分布,あるいは派生分布でよい.
- 使用可能なオプション
-
AccuracyGoal Automatic 目標確度 ParameterEstimator "MaximumLikelihood" 使用する母数推定器 PrecisionGoal Automatic 目標精度 WorkingPrecision Automatic 内部計算精度 - ParameterEstimatorには次の基本設定が使える.
-
"MaximumLikelihood" 対数尤度関数を最大化する "MethodOfMoments" 原点の周りのモーメントをマッチする "MethodOfCentralMoments" 中心モーメントをマッチする "MethodOfCumulants" キュムラントをマッチする "MethodOfFactorialMoments" 階乗モーメントをマッチする - 最尤法は対数尤度関数
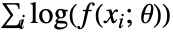 を最大化しようとする.ただし,
を最大化しようとする.ただし,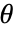 は分布母数であり
は分布母数であり 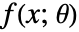 は分布の確率密度関数である.
は分布の確率密度関数である. - モーメント法は
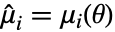 ,
, 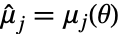 ,
,  を解くことができる.ただし,
を解くことができる.ただし,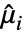 は
は 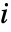
 次サンプルモーメント,
次サンプルモーメント,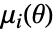 は分布の
は分布の 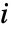
 次モーメントで,母数は
次モーメントで,母数は 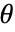 である.
である. - モーメント法に基づく推定器は母数についてのすべての制約を満たさないことがある.
例題
すべて開くすべて閉じる例 (3)
オプション (4)
ParameterEstimator (3)
アプリケーション (14)
テキスト頻度 (1)
地震のマグニチュード (1)
EstimatedDistributionをMixtureDistributionのような構造と一緒に使って多峰モデルを構築することができる:
アメリカ合衆国における1935年から1989年までの地震のマグニチュードには2つのはモードがある:
あるNormalDistributionと別の正規分布の可能な混合から分布をフィットする:
風速分析 (1)
データをRayleighDistributionにフィットする:
ExtremeValueDistributionにフィットする:
自動車の燃費 (1)
地震と地震の間隔 (1)
次のデータは1902年12月16日から1977年3月4日までに世界中で発生した大きい(マグニチュードが7.5以上もしくは死者が1000人以上の)地震から次の大きい地震までの日数を含んでいる:
ExponentialDistributionで地震の間隔をモデル化する:
地震頻度 (1)
1年間の地震の回数はSinghMaddalaDistributionでモデル化することができる:
間欠泉噴出までの時間 (1)
オールド・フェイスフル・ガイザーの噴出から次の噴出までの時間のヒストグラムには2つのモードがある:
MixtureDistributionをデータにフィットする:
出水率 (1)
マハナディ川の1日あたりの最低流量を1年ごとに計算したもの(立方メートル/秒)を考える:
1日あたりの最低流量を1年ごとに計算したものをMinStableDistributionでモデル化する:
特性と関係 (8)
EstimatedDistributionは母数推定を挿入した分布を与える:
FindDistributionParametersは母数推定を置換規則として与える:
EstimatedProcessはパラメトリック過程を推定する:
EstimatedDistributionはパラメトリック分布を推定する:
DistributionFitTestを使ってフィットの質を調べる:
EstimatedDistributionはパラメトリック分布の母数を推定する:
SmoothKernelDistributionはノンパラメトリックカーネル密度推定を与える:
ノンパラメトリック分布とパラメトリック分布の確率密度関数を比較する:
SmoothHistogramを使ってノンパラメトリック密度を可視化する:
EstimatedDistributionは母数の最尤度推定を与える:
Likelihoodを使って尤度を計算する:
LogLikelihoodを使って対数尤度を計算する:
Momentを使ってデータから原点の周りのモーメントを計算する:
QuantilePlotを使って経験的変位値とフィットされた分布変位値を可視化する:
QuantilePlot内で推定した場合について同じ可視化を行う:
EstimatedDistributionは,TimeSeriesとEventSeriesのタイムスタンプを無視する:
TemporalDataについては,すべての経路構造が無視される:
テキスト
Wolfram Research (2010), EstimatedDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/EstimatedDistribution.html.
CMS
Wolfram Language. 2010. "EstimatedDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedDistribution.html.
APA
Wolfram Language. (2010). EstimatedDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatedDistribution.html