represents a zeta distribution with parameter ρ.
ZipfDistribution[n,ρ]
represents a Zipf distribution with range n.


ZipfDistribution
represents a zeta distribution with parameter ρ.
ZipfDistribution[n,ρ]
represents a Zipf distribution with range n.
Details
- ZipfDistribution[ρ] is also known as the discrete Pareto distribution.
- ZipfDistribution[n,ρ] is also known as the Estoup distribution.
- The probability for value
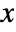 and finite
and finite 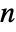 is given by
is given by ![x^(-(rho+1))/TemplateBox[{n, {rho, +, 1}}, HarmonicNumber2] x^(-(rho+1))/TemplateBox[{n, {rho, +, 1}}, HarmonicNumber2]](Files/ZipfDistribution.en/3.png) and for infinite
and for infinite 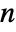 given by
given by ![x^(-(rho+1))/TemplateBox[{{rho, +, 1}}, Zeta] x^(-(rho+1))/TemplateBox[{{rho, +, 1}}, Zeta]](Files/ZipfDistribution.en/5.png) .
. - ZipfDistribution allows ρ to be any positive real number and n any positive integer.
- ZipfDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- ZipfDistribution[n,ρ] represents a discrete statistical distribution defined for integer values
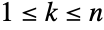 and determined by a positive real parameter ρ and by a positive integer parameter n (the range of the distribution). The Zipf distribution has a probability density function (PDF) that is discrete and monotone decreasing, and whose overall shape (its spread, its domain, and its steepness) is determined by the values of ρ and n. The Zipf distribution stated is sometimes referred to as the Estoup distribution. The one-parameter form ZipfDistribution[ρ] is equivalent to the limit of ZipfDistribution[n,ρ] as n→∞ and is most commonly referred to as "the" Zipf distribution, though it may also be referred to as the zeta distribution, Zipfian distribution, or discrete Pareto distribution (not to be confused with the continuous ParetoDistribution).
and determined by a positive real parameter ρ and by a positive integer parameter n (the range of the distribution). The Zipf distribution has a probability density function (PDF) that is discrete and monotone decreasing, and whose overall shape (its spread, its domain, and its steepness) is determined by the values of ρ and n. The Zipf distribution stated is sometimes referred to as the Estoup distribution. The one-parameter form ZipfDistribution[ρ] is equivalent to the limit of ZipfDistribution[n,ρ] as n→∞ and is most commonly referred to as "the" Zipf distribution, though it may also be referred to as the zeta distribution, Zipfian distribution, or discrete Pareto distribution (not to be confused with the continuous ParetoDistribution). - The Zipf distribution is named for American linguist George Zipf, who applied the distribution heavily in his work on behavior and psychology throughout the 1930s and 1940s. Though the distribution was studied and applied in similar contexts by French stenographer Jean-Baptiste Estoup as early as 1912, Zipf's work inspired what is now known as Zipf's law (of which the Zipf distribution is the foundation), which states that the frequency of any word in any usage of natural language is inversely proportional to its rank in the language's associated frequency table. Many modern applications of the Zipf distribution are therefore related to linguistics and semantics, though the distribution has also been applied to phenomena in number theory, biology, and economics.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Zipf distribution. Distributed[x,ZipfDistribution[n,ρ]], written more concisely as xZipfDistribution[n,ρ], can be used to assert that a random variable x is distributed according to a Zipf distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[ZipfDistribution[n,ρ],x] and CDF[ZipfDistribution[n,ρ],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Zipf distribution, EstimatedDistribution to estimate a Zipf parametric distribution from given data, and FindDistributionParameters to fit data to a Zipf distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Zipf distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Zipf distribution.
- TransformedDistribution can be used to represent a transformed Zipf distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Zipf distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Zipf distributions.
- ZipfDistribution is related to a number of other statistical distributions. It is often thought of as a discretized version of ParetoDistribution and hence is related to PowerDistribution, StableDistribution, ExponentialDistribution, PearsonDistribution, and BetaPrimeDistribution. ZipfDistribution is also related to CauchyDistribution, LevyDistribution, PoissonDistribution, PoissonConsulDistribution, and SkellamDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from a Zipf distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
In the limit, skewness is infinite:
Find where the skewness attains its minimum:
In the limit, kurtosis is infinite:
Find where the kurtosis attains its minimum:
Different moments with closed forms as functions of parameters:
Moment has closed form:
Applications (6)
CDF of ZipfDistribution is an example of a right-continuous function:
The word count in a text follows Zipf distribution:
Fit a ZipfDistribution to the word frequency data:
Compare the frequency histogram with the estimated distribution:
Find the probability that a word appears more than 10 times:
Find the average number of word occurrences:
Rank 15 web pages according to popularity. The access frequencies follow Zipf distribution with ![]() . Find the distribution of access frequencies:
. Find the distribution of access frequencies:
Find the probability of the top-ranked site request:
Find the probability of the request for one of the bottom five websites:
Simulate 30 independent requests:
An online movie rental website has 2000 titles, keeping the most popular ones in cache to provide faster service. Find the minimum number of titles that must be in cache, so that with probability 0.99, a requested movie is in the cache:
ZipfDistribution can be used to model the distribution of GCD between random numbers:
Fit a Zipf distribution to the data:
Fit a Zipf distribution with a range to the data:
Compare the histogram of the sample with both estimated distributions:
The finite range condition significantly changes the distribution statistics:
The number of dead and injured in a terrorist attack follows ZipfDistribution:
Fit a Zipf distribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Properties & Relations (7)
The probability of getting any real number except a positive integer is zero:
The probability mass and random variable have a power-law relationship:
The relative frequency of the ![]()
![]() value to the first value in Zipf distribution is the power of
value to the first value in Zipf distribution is the power of ![]() :
:
In the limit, the second value will have ![]() the frequency of the first value, the third value will have
the frequency of the first value, the third value will have ![]() the frequency of the first value, etc.:
the frequency of the first value, etc.:
Zipf distribution is closed under truncation:
Relationships to other distributions:
Both Zipf distributions become equal in the limit:
Khintchine's infinitely divisible Riemann zeta distribution is related to ZipfDistribution:
Verify that the characteristic function of ζ is the expected ratio of Riemann zeta functions:
Possible Issues (2)
ZipfDistribution is not defined when ρ is non-positive:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Related Guides
Text
Wolfram Research (2007), ZipfDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ZipfDistribution.html (updated 2010).
CMS
Wolfram Language. 2007. "ZipfDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/ZipfDistribution.html.
APA
Wolfram Language. (2007). ZipfDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZipfDistribution.html
BibTeX
@misc{reference.wolfram_2025_zipfdistribution, author="Wolfram Research", title="{ZipfDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ZipfDistribution.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_zipfdistribution, organization={Wolfram Research}, title={ZipfDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/ZipfDistribution.html}, note=[Accessed: 28-February-2026]}