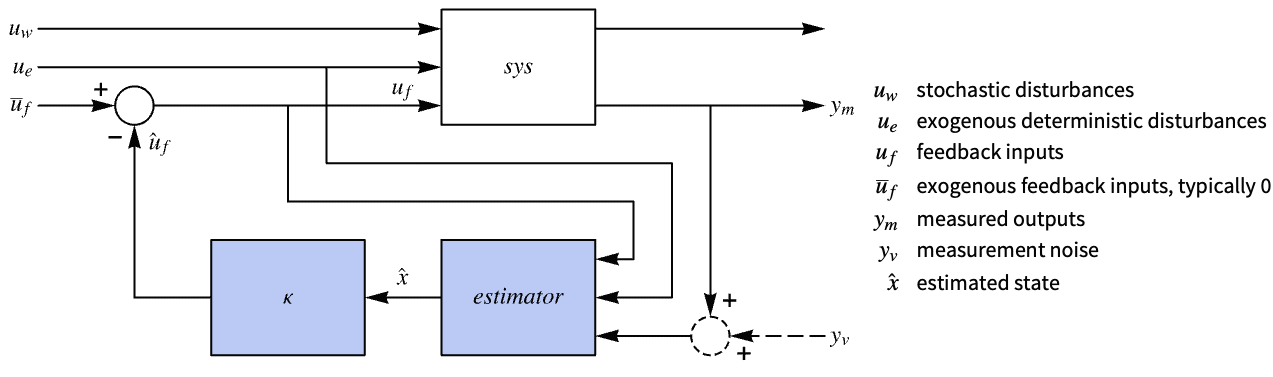
EstimatorRegulator[sspec,{l,κ}]
gives the output feedback controller with estimator and regulator gains l and κ for the system specification sspec.
EstimatorRegulator[…,"prop"]
gives the value of the property "prop".


EstimatorRegulator
EstimatorRegulator[sspec,{l,κ}]
gives the output feedback controller with estimator and regulator gains l and κ for the system specification sspec.
EstimatorRegulator[…,"prop"]
gives the value of the property "prop".
Details and Options







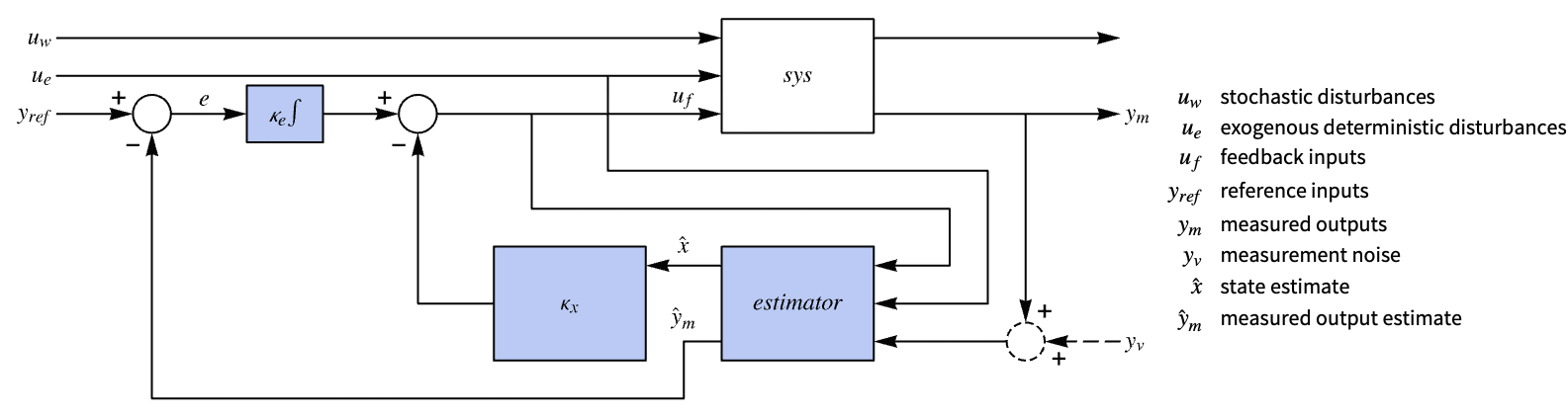
- EstimatorRegulator is also known as observer controller or estimator controller.
- EstimatorRegulator is used to assemble a control system consisting of an estimator and a regulating or tracking controller.
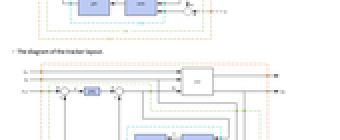
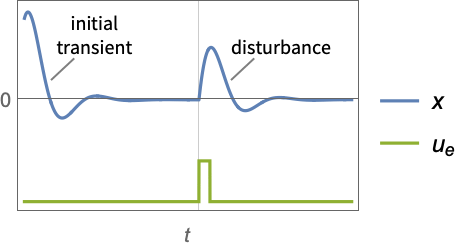
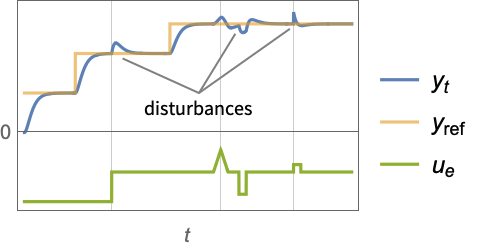
- A regulating controller aims to maintain the system at an equilibrium state despite disturbances
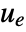 pushing it away. Typical examples include maintaining an inverted pendulum in its upright position or maintaining an aircraft in level flight.
pushing it away. Typical examples include maintaining an inverted pendulum in its upright position or maintaining an aircraft in level flight. - The regulating controller is given by a control law of the form
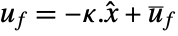 , where
, where 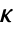 is the computed gain matrix.
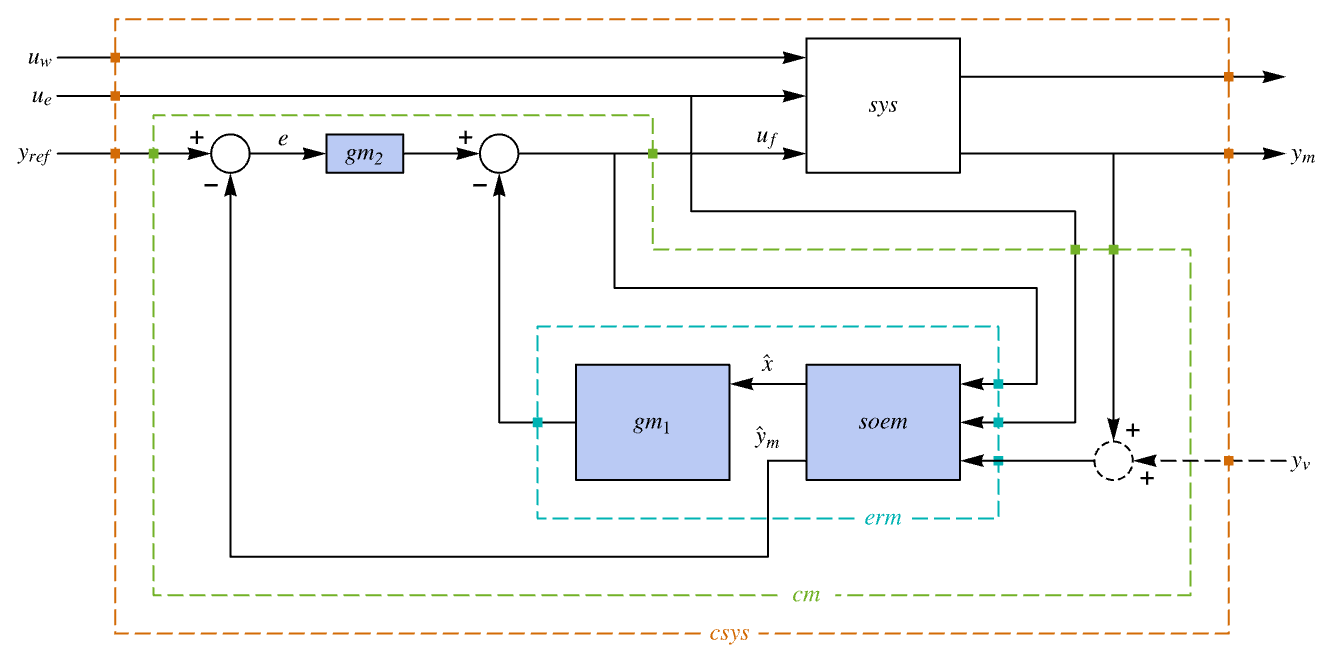
is the computed gain matrix. - A tracking controller aims to track a reference signal despite disturbances
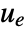 interfering with it. Typical examples include a cruise control system for a car or path tracking for a robot.
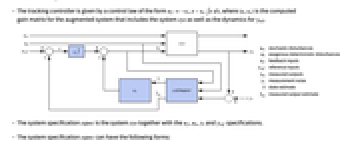
interfering with it. Typical examples include a cruise control system for a car or path tracking for a robot. - The tracking controller is given by a control law of the form
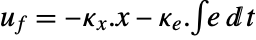 , where
, where 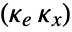 is the computed gain matrix for the augmented system that includes the system sys as well as the dynamics for
is the computed gain matrix for the augmented system that includes the system sys as well as the dynamics for 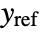 .
. - The system specification sspec is the system sys together with the uf, ue, yt and yref specifications.
- The system specification sspec can have the following forms:
-
StateSpaceModel[…] linear control input and linear state AffineStateSpaceModel[…] linear control input and nonlinear state NonlinearStateSpaceModel[…] nonlinear control input and nonlinear state SystemModel[…] general system model <|…|> detailed system specification given as an Association - The detailed system specification can have the following keys:
-
"InputModel" sys any one of the models "FeedbackInputs" All the feedback inputs uf "ExogenousInputs" None the exogenous inputs ue "MeasuredOutputs" All the measured outputs ym "TrackedOutputs" None tracked outputs yt - The inputs and outputs can have the following forms:
-
{num1,…,numn} numbered inputs or outputs numi used by StateSpaceModel, AffineStateSpaceModel and NonlinearStateSpaceModel {name1,…,namen} named inputs or outputs namei used by SystemModel All uses all inputs or outputs None uses none of the inputs or outputs - The estimator gains l can be computed using EstimatorGains, LQEstimatorGains or DiscreteLQEstimatorGains.
- The feedback gains κ can be computed using StateFeedbackGains, LQRegulatorGains, LQOutputRegulatorGains or DiscreteLQRegulatorGains.
- EstimatorRegulator[…,"Data"] returns a SystemsModelControllerData object cd that can be used to extract additional properties using the form cd["prop"].
- EstimatorRegulator[…,"prop"] can be used to directly get the value of cd["prop"].
- Possible values for properties "prop" include:
-
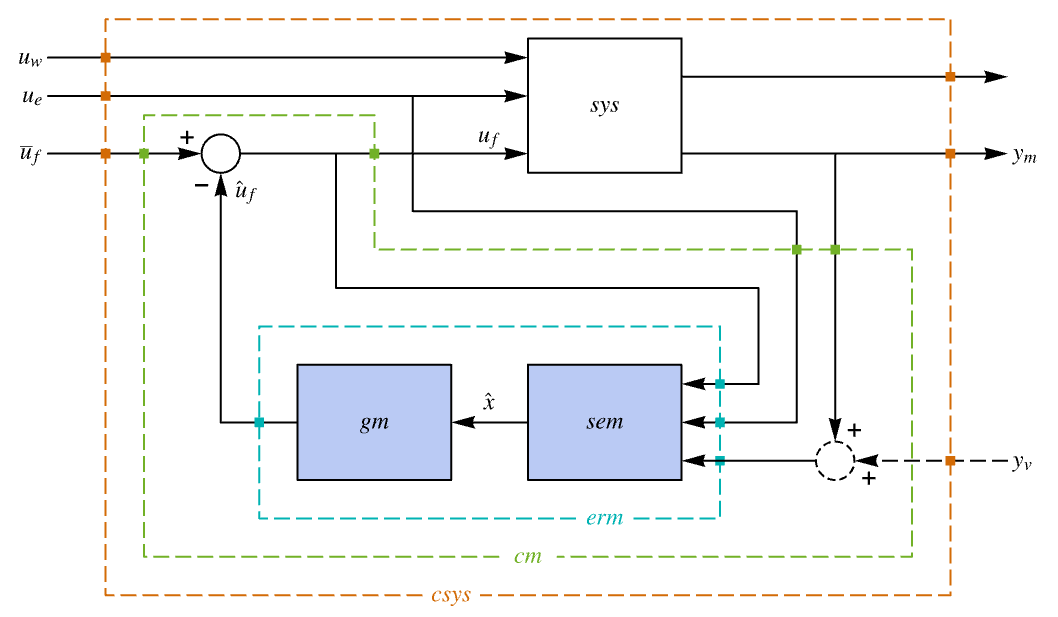
"BlockDiagram" block diagram of csys {"BlockDiagram",<|"SampledData"True|>} create a sampled data block diagram of csys "ClosedLoopPoles" poles of "ClosedLoopSystem" "ClosedLoopSystem" system csys {"ClosedLoopSystem",cspec} detailed control over the form of the closed-loop system "ControllerModel" model cm with 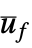 , ue, ym as input and uf as output
, ue, ym as input and uf as output"Design" type of controller design "DesignModel" model used for the design "EstimatorGains" gain matrix ℓ "EstimatorRegulatorModel" model erm "ExogenousInputs" deterministic and non-feedback inputs ue of sys "FeedbackGains" gain matrix κ or its equivalent "FeedbackGainsModel" model gm or {gm1,gm2} "FeedbackInputs" inputs uf of sys used for feedback "InputCount" number of inputs u of sys "InputModel" input model sys "MeasuredOutputs" measured outputs ym of sys "OpenLoopPoles" poles of the Taylor linearized sys "OutputCount" number of outputs y of sys "SamplingPeriod" sampling period of sys "StateCount" number of states x of sys "StateEstimatorModel" model sem "StateOutputEstimatorModel" model soem "TrackedOutputs" outputs yt of sys that are tracked - Possible keys for cspec include:
-
"InputModel" input model in csys "Merge" whether to merge csys "ModelName" name of csys "NoisyOutputs" subset of ym that are noisy "SamplingPeriod" to create a sampled data csys - The diagram of the regulator layout.
- The diagram of the tracker layout.
Examples
open all close allBasic Examples (6)
Construct an EstimatorRegulator:
An estimator regulator for a discrete-time model:
An estimator regulator for a nonlinear system:
An estimator regulator with specified measurements and feedback inputs:
An estimator regulator with optimal gains:
A set of optimal regulator gains:
Scope (31)
Basic Uses (8)
A system with one feedback input and one measurement:
The feedback input and measurement are inputs to the estimator-regulator:
A system with one noisy input as well:
Noisy inputs are not inputs to the estimator-regulator:
A system with one feedback and one exogenous input:
The exogenous input is an input to the estimator-regulator:
A system where only some of the outputs are measured:
Only the feedback input and measured output are fed to the estimator-regulator:
Compute the gains using pole placement:
Assemble the estimator-regulator:
Assemble the estimator-regulator:
Compute only the feedback gains optimally:
Compute the estimator gains using pole placement:
Assemble the estimator-regulator:
Plant Models (5)
A continuous-time StateSpaceModel:
The controller for a set of gains:
The poles of the closed-loop system:
A discrete-time StateSpaceModel:
The controller for a set of gains:
A descriptor StateSpaceModel:
The controller has the same descriptor matrix:
An AffineStateSpaceModel with a set of gains:
Its poles are that of the Taylor linearized model:
A NonlinearStateSpaceModel with a set or gains:
Properties (10)
By default, EstimatorRegulator returns the controller comprising the estimator and regulator:
The controller can also be obtained as a property:
A block diagram of the closed-loop system:
The estimator-regulator feedback model:
In this model, the feedback input is fed back directly:
Assemble the estimator and regulator with feedback to get the same result as before:
The closed-loop system differs from the computed one only in the input matrix:
Properties related to the input model and gains:
Get the controller data object:
Tracking (5)
First design a state feedback controller and estimator:
Assemble the tracking controller:
The closed-loop system tracks the reference signal ![]() :
:
A block diagram of the closed-loop system:
Design a tracking controller for a discrete-time system:
First design a state feedback controller and estimator:
Assemble the tracking controller:
The closed-loop system tracks the reference signal ![]() :
:
Design an optimal state feedback controller:
And an estimator using pole placement:
Assemble the tracking controller:
The closed-loop system tracks two different reference signals:
Compute the controller effort:
Design an optimal state feedback controller:
Assemble the tracking controller:
Track a desired reference signal:
The reference signal is of order 2:
Set the reference as the sum of sinusoids:
Design a controller to track one output of a first-order system:
The dimensions of the state weighting matrix qq are k+m q:
Compute the regulator controller:
Closed-Loop System (3)
The closed-loop system based on a nonlinear model:
Compute the closed-loop system based on the linearized design:
Compare the response of the two designs:
Assemble the merged closed-loop system of a plant with an EstimatorRegulator:
The unmerged closed-loop system:
When merged, it gives the same result as before:
Merge the closed-loop system explicitly:
Create a closed-loop system with a desired name:
The closed-loop system has the specified name:
The name can be directly used to specify the closed-loop model in other functions:
Applications (11)
Mechanical Systems (3)
Design a controller for a partially controllable double cart-spring system:
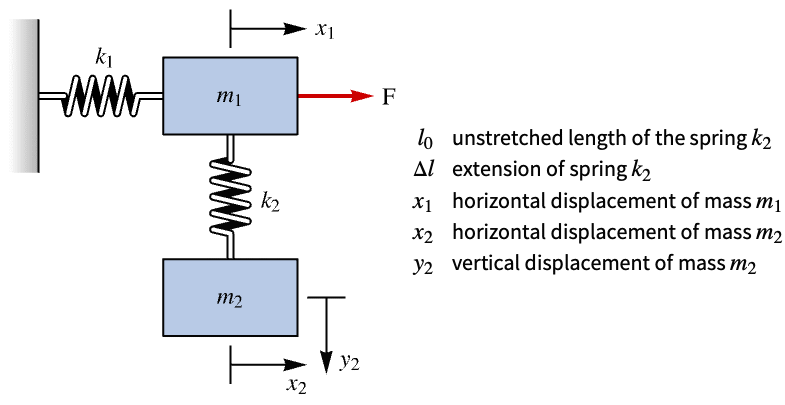
The system is not controllable:
Obtain the controllable subsystem:
The response of the open-loop system:
Compute a set of optimal feedback gains:
Assemble the estimator-regulator:
Obtain the closed-loop system:
The horizontal positions of the masses are controlled:
While the vertical position of ![]() is not:
is not:
Dampen the oscillations of a three-mass system:
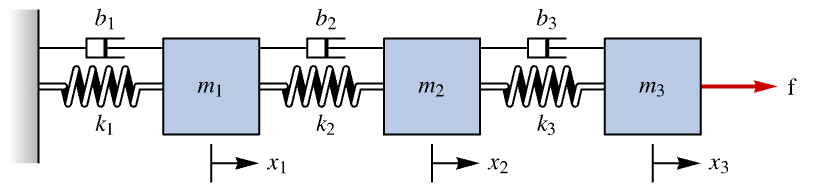
The open-loop response is highly oscillatory:
Compute a set of optimal regulator gains:
Assemble the estimator-regulator:
Obtain the closed-loop system:
The oscillations are suppressed by the feedback controller:
Dampen the oscillations of a coupled pendulum:
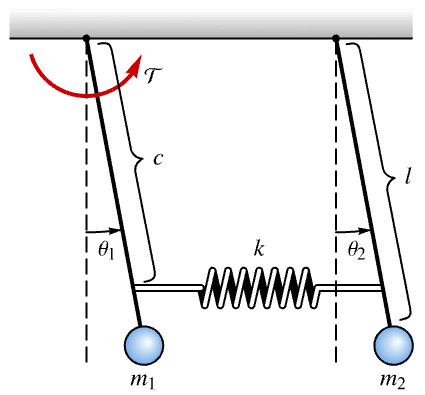
The undamped open-loop response:
Compute a set of estimator gains:
Compute a set of optimal gains:
Assemble the estimator-regulator:
Obtain the closed-loop system:
Aerospace Systems (3)
Stabilize the orbit of a spacecraft near a circular orbit of mean motion ω:
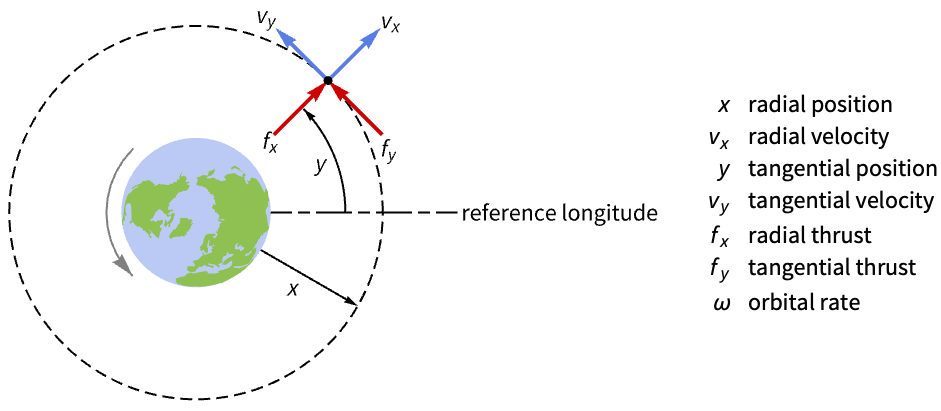
Discretize the system with a sampling time of ![]() :
:
The satellite's orbit is unregulated to a perturbation in the states:
Compute a set of regulator gains:
Assemble the estimator regulator:
Obtain the closed-loop system:
The satellite's orbit is stabilized:
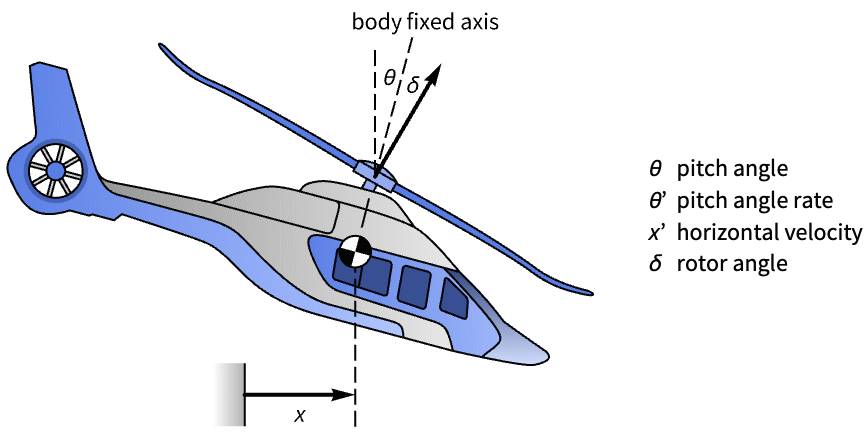
Its pole-zero plot shows it is unstable:
Compute a set of regulator gains:
Assemble the estimator regulator:
Obtain the closed-loop system:
Control a quadcopter drone’s altitude:
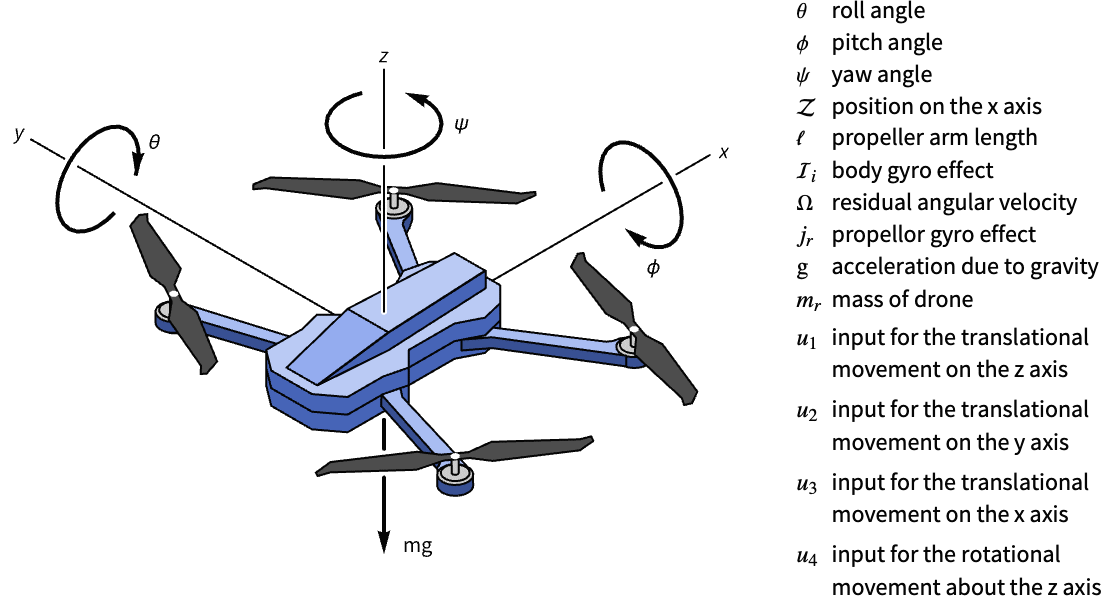
Without any input, the drone is in free fall:
A set of LQ regulator weights that consider the maximum motor voltage of ![]() v:
v:
Compute the optimal regulator:
Assemble the estimator-regulator:
Obtain the closed-loop system:
Biological Systems (1)
Regulate the blood-glucose level in the human body:

The Bergman model of the system:
The system is slow with poles close to the ![]() axis:
axis:
Hence the glucose level in the open-loop system takes a long time to settle:
Set the exogenous insulin infusion rate as the feedback input and compute a set of optimal gains:
Assemble an estimator-regulator:
Obtain the closed-loop system:
Chemical Systems (2)
Regulate the biomass concentration in an isothermal constant-volume fermenter: »

The biomass concentration of the unregulated system:
Compute a set of regulator gains:
Compute a set of estimator gains:
Assemble an estimator regulator:
The biomass concentration is regulated:
Improve the response of a mixing tank process:
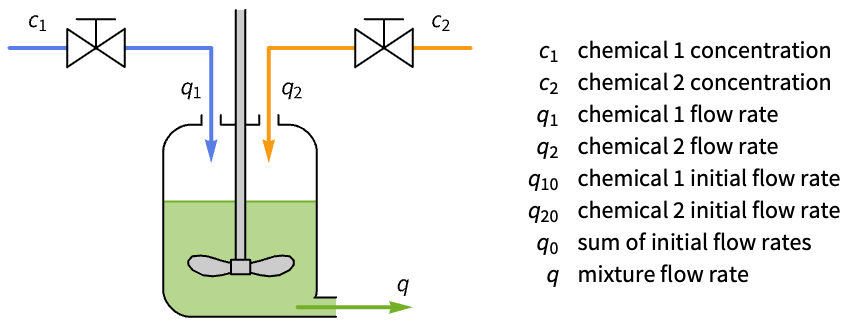
The output response takes ![]() to stabilize:
to stabilize:
The system’s fast and slow modes are controllable:
Compute a set of state feedback gains:
Obtain the closed-loop system:
The response of the closed-loop system only takes ![]() to stabilize:
to stabilize:
Electrical Systems (2)
Regulate a DC motor driven by a buck converter:
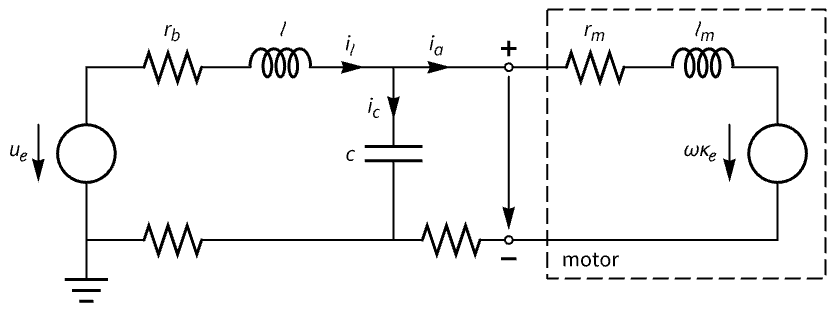
The system has poles close to the imaginary axis:
Therefore the response of the system to an initial perturbation is slow:
Compute a set of regulator gains:
Assemble the estimator regulator:
Obtain the closed-loop system:
The closed-loop response is faster:
Dampen the response of the terminal voltage of a power system:
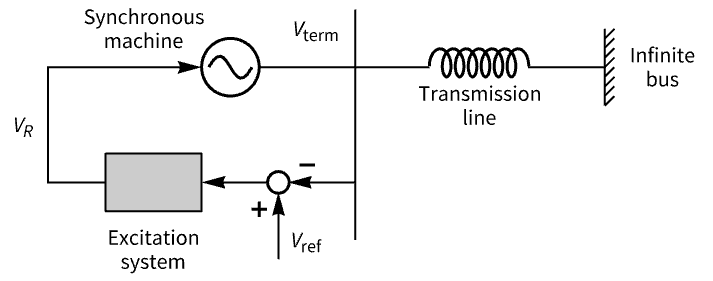
The system has two lightly damped poles:
The open-loop response is therefore highly oscillatory:
Compute a set of regulator gains:
Assemble the estimator-regulator:
Obtain the closed-loop system:
The closed-loop response to a perturbation in the synchronous machine is damped and is faster:
Properties & Relations (7)
The closed-loop poles are those of the estimator and state-feedback designs:
The poles of the estimator design:
The poles of the state-feedback design:
An estimator-regulator assembled using gains from StateFeedbackGains and EstimatorGains:
The estimator-regulator can be assembled using the gains or the controller data object:
An estimator-regulator assembled using gains from LQRegulatorGains and EstimatorGains:
A set of optimal feedback gains:
The estimator-regulator can be assembled using the gains or the controller data object:
An estimator-regulator assembled using gains from DiscreteLQRegulatorGains and DiscreteLQEstimatorGains:
A set of optimal discrete-time estimator gains:
A set of optimal discrete-time feedback gains:
LQGRegulator is assembled using EstimatorRegulator:
The uncontrollable poles of a stabilizable system are not affected by an estimator-regulator:
The stable pole ![]() is uncontrollable:
is uncontrollable:
The poles of the closed-loop system:
The uncontrollable pole is unchanged:
Larger estimator gains result in a faster response but amplify noise:
A set of state feedback gains:
A set of increasing estimator gains:
The responses of the closed-loop systems:
As the estimator gains increase, the response is faster but the effects of the noise are more pronounced:
The plot of the norm of the estimator gains versus output response:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2021 (12.3) ▪ 2021 (13.0)
Text
Wolfram Research (2010), EstimatorRegulator, Wolfram Language function, https://reference.wolfram.com/language/ref/EstimatorRegulator.html (updated 2021).
CMS
Wolfram Language. 2010. "EstimatorRegulator." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/EstimatorRegulator.html.
APA
Wolfram Language. (2010). EstimatorRegulator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatorRegulator.html
BibTeX
@misc{reference.wolfram_2025_estimatorregulator, author="Wolfram Research", title="{EstimatorRegulator}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatorRegulator.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_estimatorregulator, organization={Wolfram Research}, title={EstimatorRegulator}, year={2021}, url={https://reference.wolfram.com/language/ref/EstimatorRegulator.html}, note=[Accessed: 22-January-2026]}