ExponentialGeneratingFunction
ExponentialGeneratingFunction[expr,n,x]
数列の n![]() 番目の項が式 expr で与えられる x における指数型母関数を与える.
番目の項が式 expr で与えられる x における指数型母関数を与える.
ExponentialGeneratingFunction[expr,{n1,n2,…},{x1,x2,…}]
n1, n2, … 番目の項が expr で与えられる x1, x2, … における多次元指数型母関数を与える.
詳細とオプション

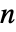
 番目の項が
番目の項が 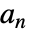 である数列の指数型母関数は
である数列の指数型母関数は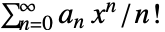 で与えられる.
で与えられる.- 多次元の指数型母関数は
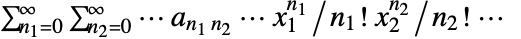 で与えられる.
で与えられる. - 使用できるオプション
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を含む答を生成するかどうか Method Automatic 使用するメソッド VerifyConvergence True 収束を確かめるかどうか
例題
すべて開くすべて閉じるスコープ (19)
基本的な用法 (6)
Plot3D,ContourPlot,またはDensityPlotを使って大きさをプロットする:
ParametricPlot3Dを使って複素平面のスペクトルをプロットする:
ExponentialGeneratingFunctionは,線形性を含む複数の特性を使用する:
ExponentialGeneratingFunctionは自動的にリストに縫い込まれる:
特殊数列 (13)
DiscreteRatioはすべての超幾何項数列について有理である:
DifferenceRootは,一般に,結果としてDifferentialRoot関数になる:
オプション (5)
GenerateConditions (1)
デフォルトで,母関数がどこで収束するかに関する条件は与えられない:
GenerateConditionsを使って妥当条件を生成する:
VerifyConvergence (3)
VerifyConvergenceをFalseに設定すると,母関数が形式オブジェクトとして扱われる:
VerifyConvergenceをTrueに設定すると,収束半径がゼロではないことが確かめられる:
さらにGenerateConditionsをTrueに設定すると,収束条件が表示される:
特性と関係 (3)
ExponentialGeneratingFunctionは事実上無限和を計算する:
考えられる問題 (1)
テキスト
Wolfram Research (2008), ExponentialGeneratingFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
CMS
Wolfram Language. 2008. "ExponentialGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html.
APA
Wolfram Language. (2008). ExponentialGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialGeneratingFunction.html