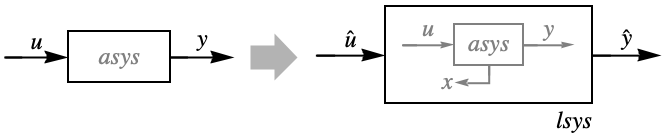
FeedbackLinearize
FeedbackLinearize[asys]
状態変換およびフィードバックでAffineStateSpaceModel asys に入出力線形化を用いる.
FeedbackLinearize[asys,{z,v}]
新たな状態 z および新たな制御入力 v を指定する.
FeedbackLinearize[asys,{z,v},"prop"]
特性"prop"を計算する.
詳細とオプション




- FeedbackLinearizeは,厳密線形化としても知られている.
- FeedbackLinearizeは,線形系 lsys についての線形制御設計の手法を使って非線形系 asys が制御できるように,非線形系 asys から線形系 lsys を構築する.
- FeedbackLinearizeはLinearizingTransformationDataオブジェクトを返す.このオブジェクトは,フィードバック線形化に基づいた分析と設計に必要な特性を抽出するために使うことができる
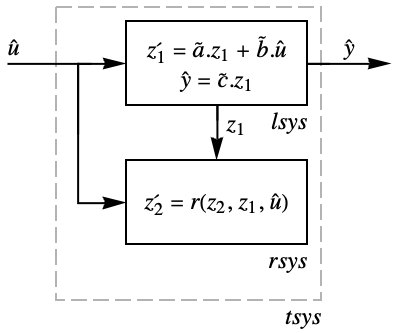
- 変換された系 tsys は,線形系 lsys からなり,残差系 rsys が含まれることもある.この残差系では,内部ダイナミクスは安定でなければならず,そうでなければ可観測ではない.
- 変換された系に関連した特性
-
"LinearSystem" 系のモデル lsys "ResidualSystem" 系のモデル rsys "TransformedSystem" 系のモデル tsys - lsys についての安定化制御器 cs を設計することで,残差系 rsys が安定であれば結果の閉ループ系も安定する.
- もとの非線形系 asys についての制御器を配備するためには,制御器 cs を変換してもとの変数を使う必要がある.
- 制御器および推定器のもとの座標への変換に関連する特性
-
{"OriginalSystemController",cs} もとの座標の制御器 cs {"OriginalSystemEstimator",es} 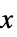 および
および 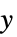 についての推定器
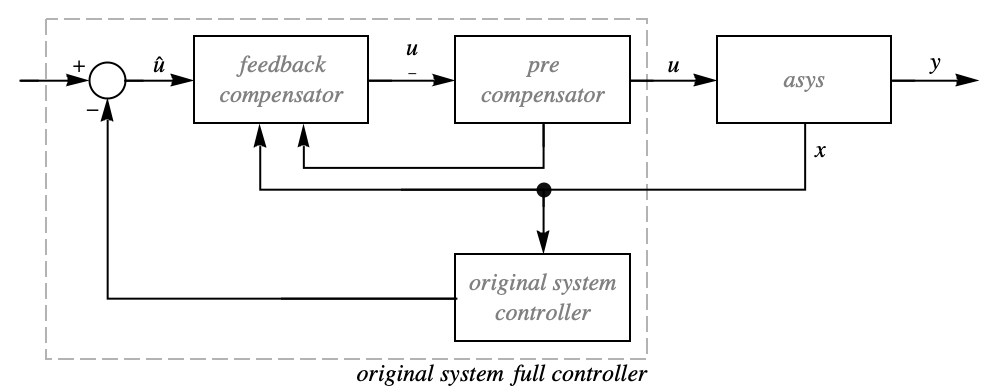
についての推定器{"ClosedLoopSystem",cs} もとの座標での閉ループ系 {"OriginalSystemFullController",cs} もとの座標での系のモデル cs - 制御器,推定器等の別のシミュレーションや実装を配備するために,フィードバック線形化についてのより詳細な特性を使うことができる.
- 系 asys
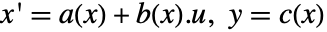 は,フィードバック補償器,前補償器,後補償器に接続されており,修正された系
は,フィードバック補償器,前補償器,後補償器に接続されており,修正された系 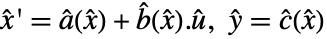 を与える.ただし,
を与える.ただし,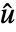 は修正入力,
は修正入力,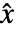 は
は 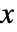 からなる状態ベクトル(補償器状態が追加されることがある),
からなる状態ベクトル(補償器状態が追加されることがある),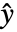 は修正出力である.
は修正出力である. - フィードバック補償器は,基本的に
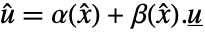 で与えられる
で与えられる 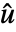 と
と 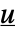 との変換である.ただし,
との変換である.ただし,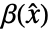 は分離行列である.
は分離行列である. - 補償器の特性
-
"FeedbackCompensator" 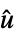 から
から 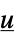 の系のモデル
の系のモデル"InverseFeedbackCompensator" 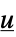 から
から 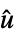 の系のモデル
の系のモデル"InverseFeedbackTransformation" 規則 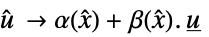 のリスト
のリスト"DecouplingMatrix" 行列 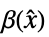
"PreCompensator" 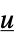 から
から 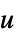 の系のモデル
の系のモデル"PostCompensator" 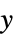 から
から 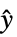 の系のモデル
の系のモデル - 明示的な線形系 lsys および可能な残差系 rsys を得るためには,状態変換
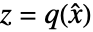 を行う必要がある.
を行う必要がある. - 状態変換およびゼロダイナミクスに関連する特性
-
"InverseStateTransformation" 規則 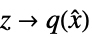 のリスト
のリスト"ZeroDynamicsSystem" 系のモデル 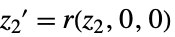
"ZeroDynamicsManifold" rsys 状態がそれについて進化した多様体 - FeedbackLinearizeは,次の設定のMethodオプションを取る.
-
Automatic 自動的にメソッドを決定する(デフォルト) "Identity" 恒等変換を伴うアイデンティティフィードバックを適用する "Burnovsky" Burnovsky形の lsys を返す

例題
すべて開くすべて閉じるスコープ (21)
基本的な用法 (5)
補償器の特性 (5)
オプション (2)
アプリケーション (8)
電気機械系 (2)
厳密線形化を使って磁気浮上系を安定させる制御器を設計し,近似線形化による設計と比較する:
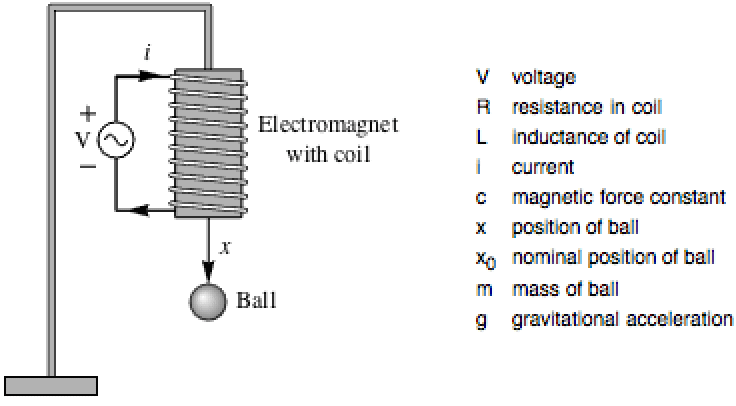
フィードバックのない系は不安定である.ここでは初期値{0.2,0.,0.1}を使う:
これには残差ダイナミクスがないので,完全にフィードバック線形化が可能である:
初期値{0.3,0.,0.31305}で系のシミュレーションを行う:
2個の直流ホイールモーターへの電圧を入力として使い,二輪倒立振子(例:セグウェイ)のための安定制御器を求める:
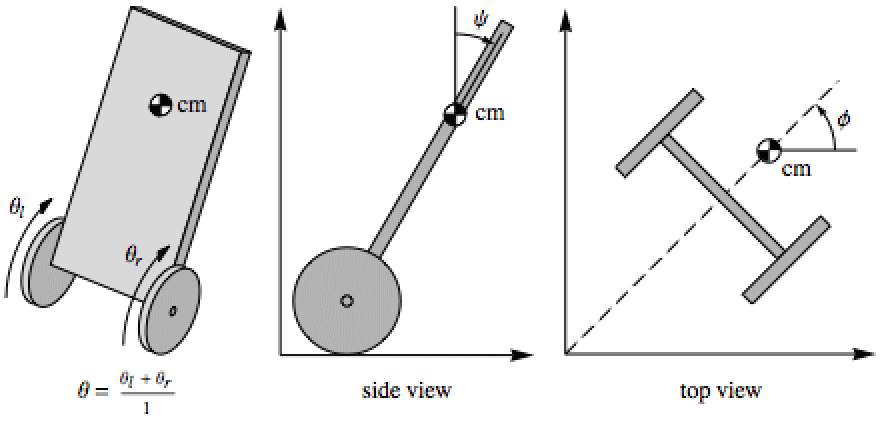
状態{θ,θ',ψ,ψ',ϕ,ϕ'}の系のAffineStateSpaceModel:
機械系 (2)
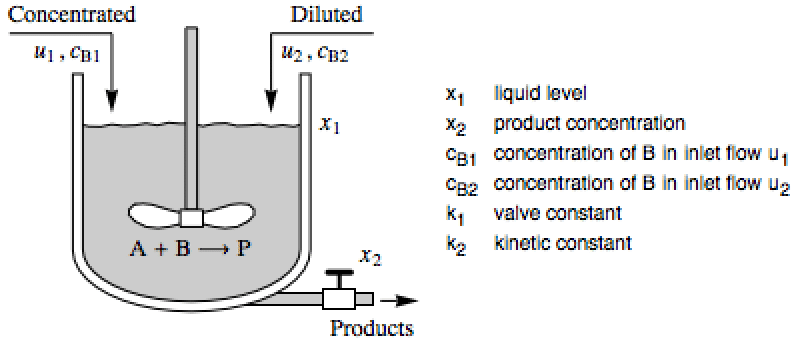
化学系 (2)
電気系 (2)
変化する負荷に依存する誘導電動機の速度応答を改善するための制御器を設計する:»

シミュレーションは,角速度に対するトルクの効果を示している:
さまざまなトルク値について,閉ループ系のシミュレーションを行う:
テキスト
Wolfram Research (2014), FeedbackLinearize, Wolfram言語関数, https://reference.wolfram.com/language/ref/FeedbackLinearize.html.
CMS
Wolfram Language. 2014. "FeedbackLinearize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FeedbackLinearize.html.
APA
Wolfram Language. (2014). FeedbackLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FeedbackLinearize.html