Fourier

Fourier[list]

求由复数组成的列表的离散傅里叶变换.

Fourier[list,{p1,p2,…}]

返回离散傅里叶变换的指定位置.

更多信息和选项

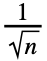
  • 长度为 n 的一个列表 ur 的离散傅里叶变换 vs 在默认情况下定义为 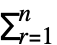ure2π i(r-1)(s-1)/n. »
  • 注意，频率为 0 的项出现在结果列表的位置 1.
  • 其它定义用在一些科学技术领域.
  • 不同的定义选择可以用选项 FourierParameters 进行设置.
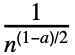
  • 在设置 FourierParameters->{a,b} 下，由 Fourier 计算所得的离散傅里叶变换是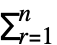ure2π i b(r-1)(s-1)/n. »
  • {a,b} 的一些通用选择是 {0,1} (默认)、{-1,1} (数据分析)、{1,-1} (信号处理).
  • 设置 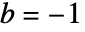实际上相应于对输入和输出列表求共轭.
  • 为了保证傅里叶逆变换的唯一性，b必须与 n 互素. »
  • 给 Fourier 的数据列表不必有等于2的幂的长度.
  • 在 Fourier[list] 中给出的 list 可以嵌套表示，以表达一个任何维数的数据数组.
  • 数据组必须是矩阵数组.
  • 如果 list 的元素是精确数，Fourier 通过对它们应用 N 来开始.
  • Fourier[list,{p1,p2,…}] 通常相当于 Extract[Fourier[list],{p1,p2,…}]. 对于仅具有几个位置 p 的情况，计算所用的算法花费的时间和内存较少，但较容易产生数值误差，尤其是当 list 的长度较大时.
  • Fourier 可用于 SparseArray 对象.

范例

打开所有单元关闭所有单元

基本范例  (2)

求一个离散的傅里叶转换：

求一个幂功率谱：

范围  (3)

x 是实数值列表：

用机器精度计算傅里叶变换：

用 24 位精度算法的计算：

计算一个二维傅里叶变换：

x 是对角线非零的 3 阶张量：

计算三维傅里叶变换：

选项  (2)

FourierParameters  (2)

无正规化：

用 正规化：

用 正规化：

干扰下 Sinc 函数的数据：

无正规化的普通功率谱：

部分功率谱：

应用  (10)

计算功率谱  (6)

“白色噪音”的傅里叶功率谱：

显示对数功率谱，包含第一个 (DC) 组件：

一个“脉冲”的功率谱是完全平坦的：

Thue–Morse 嵌套序列的幂功率谱 [更多信息]：

斐波那契（ Fibonacci ）嵌套序列的幂功率谱 [更多信息]：

一个嵌套模式的二维幂功率谱：

绘制嵌套模式：

求对数的幂功率谱：

求规则 30 的元胞自动机的傅里叶变换：

对数幂功率谱：

滤波数据  (1)

对一个平滑的间断函数，计算离散循环卷积：

计算循环卷积：

显示原始的和平滑的函数：

卷积与 ListConvolve 一致：

频率识别  (1)

下面是有某些噪音的周期数据：

找到频谱中的最大模式：

获取与正频率对应的位置，并在频谱图上显示位置：

在找到的最大模式之间，求高解析度的频谱：

确定频率周期：

计算特征向量  (1)

m 是一个循环微分矩阵：

因为 ，m 的特征值是：

特征向量是 DFT 矩阵的列，因此傅里叶对角化 m：

这对于特定向量，允许 MatrixExp[m,r] 的有效计算：

在单位间隔内，显示热方程 的近似变化：

分数傅里叶变换  (1)

使用 FourierParameters 的不同选择，定义分数傅里叶变换：

属性和关系  (6)

InverseFourier 是 Fourier 的逆：

对于实数输入，第一个之后的所有元素是以复数共轭对的形式出现：

幂频谱是对称的：

对应傅里叶变换乘法的循环卷积：

由 给出：

Fourier 等于 FourierMatrix:

矩阵的共轭转换等于 InverseFourier：

可能存在的问题  (4)

如果 与 不是互质的，转换不可逆：

长度是2的幂或可因式分解成小素数的积，速度会比较快：

当只需要很小数目的系数时，Fourier 使用有效的算法：

快速、高效的执行可能会导致显著的数值误差：

Wolfram Research (1988)，Fourier，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Fourier.html （更新于 2012 年）.

文本

Wolfram Research (1988)，Fourier，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Fourier.html （更新于 2012 年）.

CMS

Wolfram 语言. 1988. "Fourier." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2012. https://reference.wolfram.com/language/ref/Fourier.html.

APA

Wolfram 语言. (1988). Fourier. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Fourier.html 年

BibTeX

@misc{reference.wolfram_2024_fourier, author="Wolfram Research", title="{Fourier}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Fourier.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourier, organization={Wolfram Research}, title={Fourier}, year={2012}, url={https://reference.wolfram.com/language/ref/Fourier.html}, note=[Accessed: 22-November-2024 ]}