PeriodogramArray[list]
returns the squared magnitude of the discrete Fourier transform (power spectrum) of list.
PeriodogramArray[list,n]
averages the power spectra of non-overlapping partitions of length n.
PeriodogramArray[list,n,d]
uses partitions with offset d.
PeriodogramArray[list,n,d,wfun]
applies a smoothing window wfun to each partition.
PeriodogramArray[list,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.
PeriodogramArray[image,…]
returns the squared power spectrum of image.
PeriodogramArray[audio,…]
returns the squared power spectrum of audio.
PeriodogramArray[video,…]
returns the squared power spectrum of the first audio track in video.


PeriodogramArray
PeriodogramArray[list]
returns the squared magnitude of the discrete Fourier transform (power spectrum) of list.
PeriodogramArray[list,n]
averages the power spectra of non-overlapping partitions of length n.
PeriodogramArray[list,n,d]
uses partitions with offset d.
PeriodogramArray[list,n,d,wfun]
applies a smoothing window wfun to each partition.
PeriodogramArray[list,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.
PeriodogramArray[image,…]
returns the squared power spectrum of image.
PeriodogramArray[audio,…]
returns the squared power spectrum of audio.
PeriodogramArray[video,…]
returns the squared power spectrum of the first audio track in video.
Details and Options

- PeriodogramArray works with numeric arrays of any rank, 2D and 3D images, and sound objects.
- In PeriodogramArray[list,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between
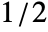 and
and 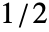 or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
or a list of length n. The default window is DirichletWindow, which effectively does no smoothing. - PeriodogramArray[list,n] is equivalent to PeriodogramArray[list,n,n,DirichletWindow,n].
- PeriodogramArray[list,{n1,n2,…}] partitions a nested list into blocks of size n1×n2×….
- For multidimensional arrays, n is taken to be equivalent to {n,n,…}.
- PeriodogramArray works with numeric lists, as well as Audio and Sound objects.
- For multichannel sounds and images, PeriodogramArray is computed for each channel separately.
- PeriodogramArray accepts the FourierParameters option. The default setting is FourierParameters->{0,1}.
Examples
open all close allBasic Examples (3)
Scope (5)
Options (1)
Properties & Relations (4)
Verification of Parseval's theorem:
Comparison with ListFourierSequenceTransform:
With partitions longer than the list, a zero-padded version of the list is used:
Use logarithmic scaling to visualize the power spectra of an image:
See Also
Periodogram ImagePeriodogram Fourier Partition SpectrogramArray DirichletWindow
Function Repository: IrregularPeriodogram WelchSpectralEstimate
Related Guides
History
Introduced in 2012 (9.0) | Updated in 2014 (10.0) ▪ 2016 (11.0) ▪ 2024 (14.1)
Text
Wolfram Research (2012), PeriodogramArray, Wolfram Language function, https://reference.wolfram.com/language/ref/PeriodogramArray.html (updated 2024).
CMS
Wolfram Language. 2012. "PeriodogramArray." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PeriodogramArray.html.
APA
Wolfram Language. (2012). PeriodogramArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PeriodogramArray.html
BibTeX
@misc{reference.wolfram_2025_periodogramarray, author="Wolfram Research", title="{PeriodogramArray}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PeriodogramArray.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_periodogramarray, organization={Wolfram Research}, title={PeriodogramArray}, year={2024}, url={https://reference.wolfram.com/language/ref/PeriodogramArray.html}, note=[Accessed: 24-February-2026]}