FractionalGaussianNoiseProcess[μ,σ,h]
represents a fractional Gaussian noise process with drift μ, volatility σ, and Hurst index h.
FractionalGaussianNoiseProcess[h]
represents a fractional Gaussian noise process with drift 0, volatility 1, and Hurst index h.


FractionalGaussianNoiseProcess
FractionalGaussianNoiseProcess[μ,σ,h]
represents a fractional Gaussian noise process with drift μ, volatility σ, and Hurst index h.
FractionalGaussianNoiseProcess[h]
represents a fractional Gaussian noise process with drift 0, volatility 1, and Hurst index h.
Details
- FractionalGaussianNoiseProcess is a continuous-time and continuous-state random process.
- FractionalGaussianNoiseProcess is a Gaussian process with mean function
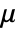 and covariance function
and covariance function ![sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2 sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2](Files/FractionalGaussianNoiseProcess.en/2.png) .
. - FractionalGaussianNoiseProcess[μ,σ,h] is equivalent to TransformedProcess[x[t+1]-x[t],xFractionalBrownianMotionProcess[μ,σ,h],t].
- FractionalGaussianNoiseProcess allows μ to be any real number, σ to be any positive real number, and h to be a real number between 0 and 1.
- FractionalGaussianNoiseProcess can be used with such functions as RandomFunction and CovarianceFunction.
Examples
open all close allBasic Examples (3)
Scope (11)
Basic Uses (6)
Process Slice Properties (5)
Univariate SliceDistribution:
First-order probability density function does not depend on time:
Compare with the density function of a normal distribution:
Multivariate slice distribution:
Slice distribution of higher order will not autoevaluate:
Compute the expectation of an expression:
Calculate the probability of an event:
Skewness and kurtosis are constant:
CentralMoment and its generating function:
Cumulant and its generating function:
Applications (1)
Properties & Relations (7)
FractionalGaussianNoiseProcess is weakly stationary:
Fractional Gaussian noise process is mean ergodic:
The process is weakly stationary:
Calculate absolute correlation function:
Find value of the strip integral:
Check if the limit of the integral is 0 to conclude mean ergodicity:
Fractional Gaussian noise does not have independent increments for ![]() :
:
Compare to the product of expectations:
Fractional Gaussian noise has a long memory for a Hurst parameter greater than 1/2:
Covariance function for a long memory process is not summable:
For a short memory, process is summable:
Conditional cumulative probability distribution:
Fractional Gaussian noise is self-similar:
Calculate scaled sums of each path:
Compare to the slice distribution of the process:
Probability density histogram and functions:
Compare to non-weakly stationary FractionalBrownianMotionProcess:
Neat Examples (3)
Simulate a fractional Gaussian noise process in two dimensions:
Study the behavior of fractional Gaussian noise depending on the Hurst parameter:
Simulate paths from a fractional Gaussian noise process:
Take a slice at 1 and visualize its distribution:
Plot paths and histogram distribution of the slice distribution at 1:
Related Guides
History
Text
Wolfram Research (2014), FractionalGaussianNoiseProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
CMS
Wolfram Language. 2014. "FractionalGaussianNoiseProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
APA
Wolfram Language. (2014). FractionalGaussianNoiseProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html
BibTeX
@misc{reference.wolfram_2025_fractionalgaussiannoiseprocess, author="Wolfram Research", title="{FractionalGaussianNoiseProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_fractionalgaussiannoiseprocess, organization={Wolfram Research}, title={FractionalGaussianNoiseProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html}, note=[Accessed: 06-March-2026]}