FresnelF
✖
FresnelF
例題
すべて開くすべて閉じる例 (4)基本的な使用例
スコープ (32)標準的な使用例のスコープの概要
数値評価 (5)
https://wolfram.com/xid/0bimmcvu-fwug8e
https://wolfram.com/xid/0bimmcvu-gctvu8
https://wolfram.com/xid/0bimmcvu-cjypew
FresnelFを高精度で効率よく評価する:
https://wolfram.com/xid/0bimmcvu-di5gcr

https://wolfram.com/xid/0bimmcvu-bq2c6r
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
https://wolfram.com/xid/0bimmcvu-73ttq
https://wolfram.com/xid/0bimmcvu-lmyeh7
https://wolfram.com/xid/0bimmcvu-i86jgd
Aroundを使って平均的な場合の統計区間を計算することもできる:
https://wolfram.com/xid/0bimmcvu-cw18bq
https://wolfram.com/xid/0bimmcvu-thgd2
MatrixFunctionを使って行列のFresnelF関数を計算することもできる:
https://wolfram.com/xid/0bimmcvu-o5jpo
特定の値 (3)
https://wolfram.com/xid/0bimmcvu-cgex6s
https://wolfram.com/xid/0bimmcvu-bdij6w
https://wolfram.com/xid/0bimmcvu-drqkdo
https://wolfram.com/xid/0bimmcvu-f2hrld
https://wolfram.com/xid/0bimmcvu-ba5463
可視化 (2)
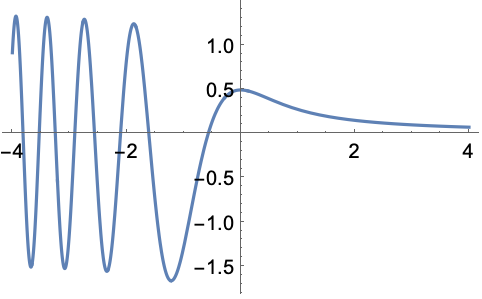
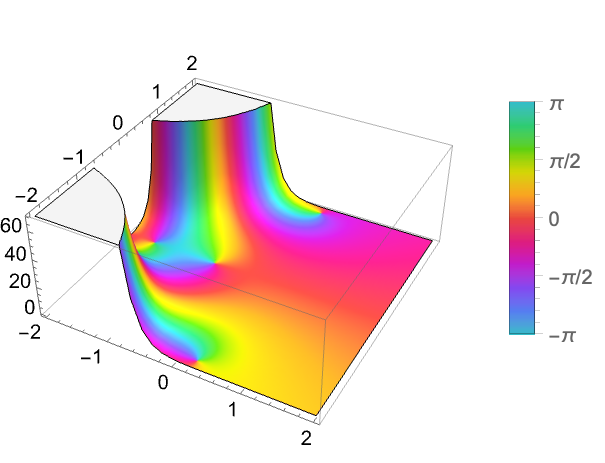
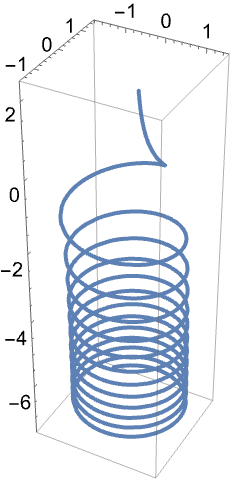
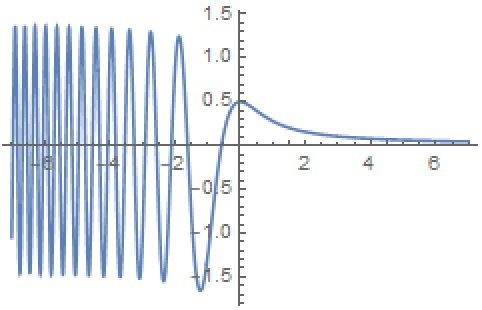
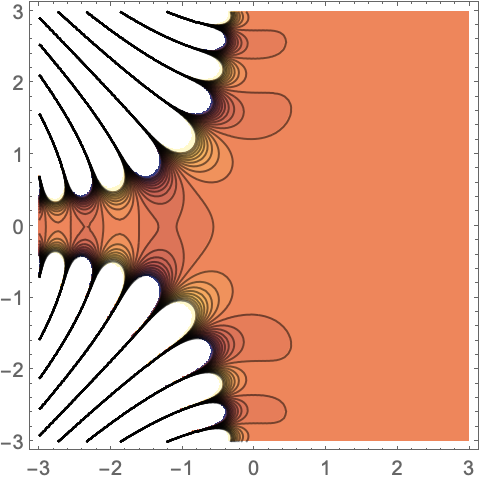
FresnelF関数をプロットする:
https://wolfram.com/xid/0bimmcvu-ecj8m7
https://wolfram.com/xid/0bimmcvu-ouu484
https://wolfram.com/xid/0bimmcvu-ixzcc6
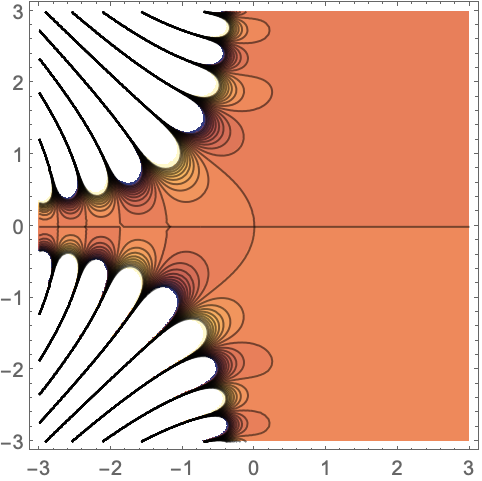
関数の特性 (9)
FresnelFはすべての実数値と複素数値について定義される:
https://wolfram.com/xid/0bimmcvu-cl7ele
https://wolfram.com/xid/0bimmcvu-de3irc
FresnelFの値域を近似する:
https://wolfram.com/xid/0bimmcvu-evf2yr
FresnelFは x の解析関数である:
https://wolfram.com/xid/0bimmcvu-h5x4l2
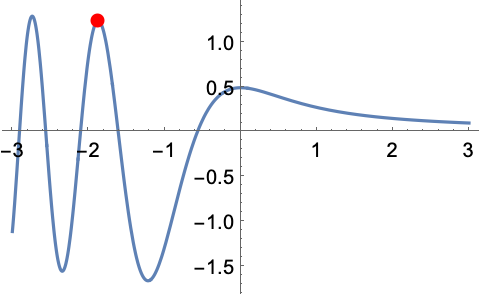
FresnelFは特定の範囲で単調である:
https://wolfram.com/xid/0bimmcvu-g6kynf
https://wolfram.com/xid/0bimmcvu-nlz7s
FresnelFは単射ではない:
https://wolfram.com/xid/0bimmcvu-gi38d7
https://wolfram.com/xid/0bimmcvu-ctca0g
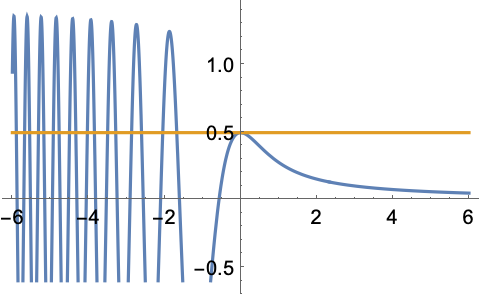
FresnelFは全射ではない:
https://wolfram.com/xid/0bimmcvu-hkqec4
https://wolfram.com/xid/0bimmcvu-hdm869
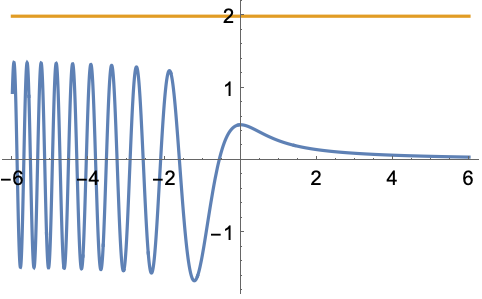
FresnelFは非負でも非正でもない:
https://wolfram.com/xid/0bimmcvu-84dui
FresnelFは特異点も不連続点も持たない:
https://wolfram.com/xid/0bimmcvu-mdtl3h
https://wolfram.com/xid/0bimmcvu-mn5jws
https://wolfram.com/xid/0bimmcvu-kdss3
微分と積分 (5)
https://wolfram.com/xid/0bimmcvu-mmas49
https://wolfram.com/xid/0bimmcvu-nfbe0l

https://wolfram.com/xid/0bimmcvu-fxwmfc
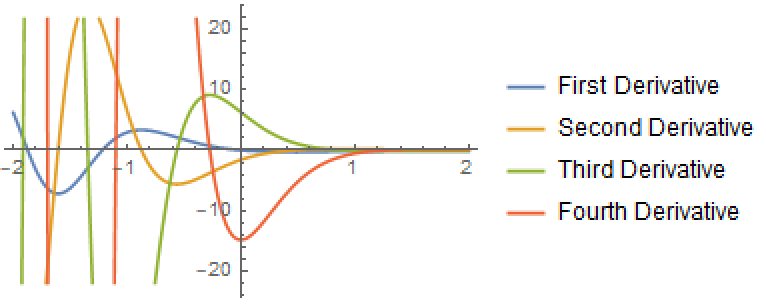
FresnelFの不定積分:
https://wolfram.com/xid/0bimmcvu-bponid
https://wolfram.com/xid/0bimmcvu-cf948
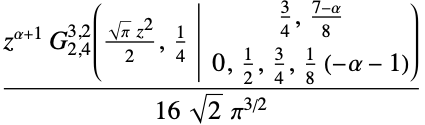
https://wolfram.com/xid/0bimmcvu-fcaobo
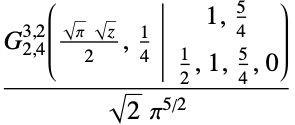
FresnelFの定積分の近似:
https://wolfram.com/xid/0bimmcvu-b9jw7l
級数展開 (4)
FresnelFのテイラー(Taylor)展開:
https://wolfram.com/xid/0bimmcvu-ewr1h8
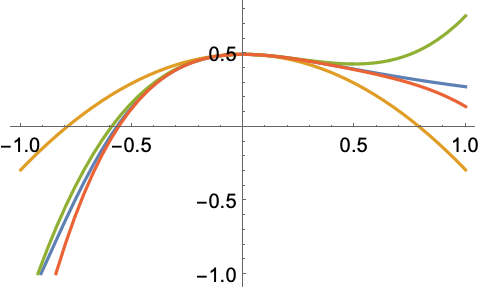
![]() の周りのFresnelFの最初の3つの近似をプロットする:
の周りのFresnelFの最初の3つの近似をプロットする:
https://wolfram.com/xid/0bimmcvu-binhar
生成点におけるFresnelFのテイラー展開:
https://wolfram.com/xid/0bimmcvu-y5gz3
https://wolfram.com/xid/0bimmcvu-eyiujb
https://wolfram.com/xid/0bimmcvu-hfjwwv
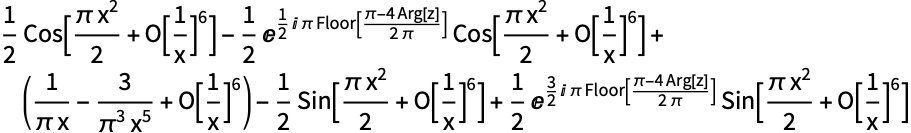
関数の恒等式と簡約 (2)
その他の特徴 (2)
FresnelFは要素単位でリストと行列に縫い込まれる:
https://wolfram.com/xid/0bimmcvu-f1ftoj
https://wolfram.com/xid/0bimmcvu-do0xrl
TraditionalFormによる表示:
https://wolfram.com/xid/0bimmcvu-4ri6xn
アプリケーション (3)この関数で解くことのできる問題の例
https://wolfram.com/xid/0bimmcvu-bmvkiq
https://wolfram.com/xid/0bimmcvu-fl5keb
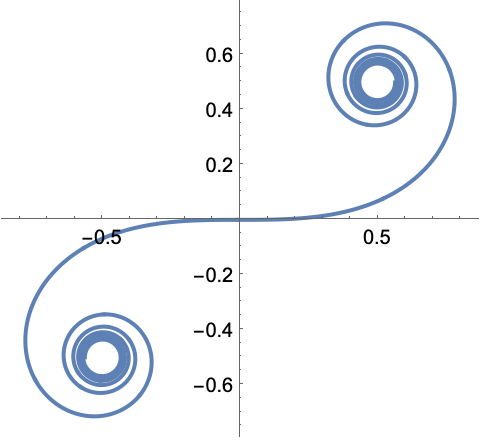
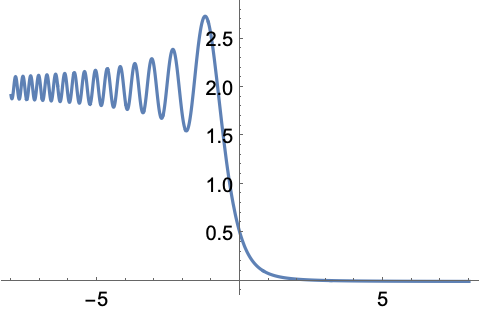
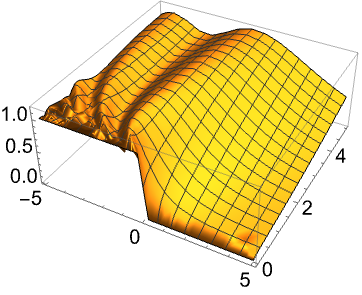
シャッターが突然開いた場合についての,時間依存1Dシュレーディンガー(Schrödinger)方程式の解:

https://wolfram.com/xid/0bimmcvu-f01ysn
https://wolfram.com/xid/0bimmcvu-c4guae
https://wolfram.com/xid/0bimmcvu-epgxic
Wolfram Research (2014), FresnelF, Wolfram言語関数, https://reference.wolfram.com/language/ref/FresnelF.html.テキスト
Wolfram Research (2014), FresnelF, Wolfram言語関数, https://reference.wolfram.com/language/ref/FresnelF.html.
Wolfram Research (2014), FresnelF, Wolfram言語関数, https://reference.wolfram.com/language/ref/FresnelF.html.CMS
Wolfram Language. 2014. "FresnelF." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FresnelF.html.
Wolfram Language. 2014. "FresnelF." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FresnelF.html.APA
Wolfram Language. (2014). FresnelF. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FresnelF.html
Wolfram Language. (2014). FresnelF. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FresnelF.htmlBibTeX
@misc{reference.wolfram_2025_fresnelf, author="Wolfram Research", title="{FresnelF}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FresnelF.html}", note=[Accessed: 01-June-2025
]}BibLaTeX
@online{reference.wolfram_2025_fresnelf, organization={Wolfram Research}, title={FresnelF}, year={2014}, url={https://reference.wolfram.com/language/ref/FresnelF.html}, note=[Accessed: 01-June-2025
]}