FresnelC[z]
gives the Fresnel integral ![]() .
.




FresnelC
FresnelC[z]
gives the Fresnel integral ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- FresnelC[z] is given by
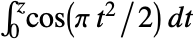 .
. - FresnelC[z] is an entire function of z with no branch cut discontinuities.
- For certain special arguments, FresnelC automatically evaluates to exact values.
- FresnelC can be evaluated to arbitrary numerical precision.
- FresnelC automatically threads over lists.
- FresnelC can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (5)
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (41)
Numerical Evaluation (5)
Evaluate numerically to high precision:
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate FresnelC efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix FresnelC function using MatrixFunction:
Visualization (2)
Function Properties (10)
FresnelC is defined for all real and complex values:
Approximate function range of FresnelC:
FresnelC is an odd function:
FresnelC is an analytic function of x:
FresnelC is neither non-increasing nor non-decreasing:
FresnelC is not injective:
FresnelC is not surjective:
FresnelC is neither non-negative nor non-positive:
FresnelC has no singularities or discontinuities:
Integration (3)
Indefinite integral of FresnelC:
Definite integral of an odd integrand over an interval centered at the origin is 0:
Series Expansions (5)
Integral Transforms (2)
Function Identities and Simplifications (3)
Verify an identity relating HypergeometricPFQ to FresnelC:
Simplify an integral to FresnelC:
Function Representations (5)
Relation to the error function Erf:
FresnelC can be represented as a DifferentialRoot:
FresnelC can be represented in terms of MeijerG:
TraditionalForm formatting:
Applications (5)
Intensity of a wave diffracted by a half‐plane:
A solution of the time‐dependent 1D Schrödinger equation for a sudden opening of a shutter:
Check the Schrödinger equation:
Plot the time‐dependent solution:
Plot of FresnelC along a circle in the complex plane:
Fractional derivative of Sin:
Derivative of order ![]() of Sin:
of Sin:
Plot a smooth transition between the derivative and integral of Sin:
Properties & Relations (6)
Use FullSimplify to simplify expressions containing Fresnel integrals:
Obtain FresnelC from integrals and sums:
Solve a differential equation:
Compare with Wronskian:
Possible Issues (3)
FresnelC can take large values for moderate‐size arguments:
A larger setting for $MaxExtraPrecision can be needed:
Some references use a different convention for the Fresnel integrals:
See Also
Tech Notes
Related Guides
Related Links
History
Introduced in 1996 (3.0) | Updated in 2014 (10.0) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1996), FresnelC, Wolfram Language function, https://reference.wolfram.com/language/ref/FresnelC.html (updated 2022).
CMS
Wolfram Language. 1996. "FresnelC." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/FresnelC.html.
APA
Wolfram Language. (1996). FresnelC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FresnelC.html
BibTeX
@misc{reference.wolfram_2025_fresnelc, author="Wolfram Research", title="{FresnelC}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/FresnelC.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_fresnelc, organization={Wolfram Research}, title={FresnelC}, year={2022}, url={https://reference.wolfram.com/language/ref/FresnelC.html}, note=[Accessed: 25-February-2026]}