WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FunctionContinuous

FunctionContinuous[f,x]

が x∈Realsについて実数値連続関数かどうかを調べる．

FunctionContinuous[f,x,dom]

が x∈dom について連続関数かどうかを調べる．

FunctionContinuous[{f₁,f₂,…},{x₁,x₂,…},dom]

が x₁,x₂,…∈dom について連続関数かどうかを調べる．

FunctionContinuous[{funs,cons},xvars,dom]

が制約条件 cons で制限された xvars∈dom について連続関数かどうかを調べる．

詳細とオプション

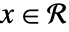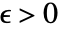すべてのとすべてのについて，すべての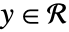についてがを含意するような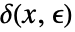が存在するなら，関数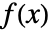は集合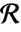において連続である．
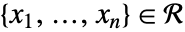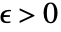すべてのとすべてのについて，すべての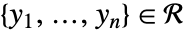について $TemplateBox[{{{, {{{x, _, 1}, -, {y, _, 1}}, ,, ..., ,, {{x, _, n}, -, {y, _, n}}}, }}}, Norm]<delta({x_1,...,x_n},epsilon)$ が $TemplateBox[{{{f, (, {{, {{x, _, 1}, ,, ..., ,, {x, _, n}}, }}, )}, -, {f, (, {{, {{y, _, 1}, ,, ..., ,, {y, _, n}}, }}, )}}}, Abs]<epsilon$ を含意するような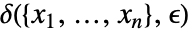が存在するなら，関数は集合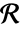において連続である．
funs に xvars 以外のパラメータが含まれているなら，結果は，通常は，ConditionalExpressionである．
dom の可能な値はRealsとComplexesである．デフォルトはRealsである．
dom がRealsなら，すべての変数，パラメータ，定数，関数の値は実数であるように制限される．
cons には，等式，不等式，それらの論理結合が含まれていてよい．
関数 funs は制約条件 cons を満足するすべての値について定義されなければならない．
次は，使用可能なオプションである．

	Assumptions	$Assumptions	パラメータについての仮定
	GenerateConditions	True	パラメータについての条件を生成するかどうか
	PerformanceGoal	$PerformanceGoal	速度と品質のどちらを優先させるか

次は，GenerateConditionsの可能な設定である．
Automatic 一般的ではない条件のみ

True すべての条件

False 条件なし

None 条件が必要な場合は未評価で返す
PerformanceGoalの可能な値には"Speed"と"Quality"がある．

例題

すべて開くすべて閉じる

例 (4)

実関数の連続性を検証する：

複素関数の連続性を検証する：

限定された領域上で連続性を検証する：

多変量関数の連続性を検証する：

スコープ (6)

一変量実関数：

一変量複素関数：

領域が限定されている関数：

多変量実関数：

多変量複素関数：

記号パラメータの関数：

オプション (4)

Assumptions (1)

FunctionContinuousはパラメータの任意の値については答を求められない：

という仮定があればFunctionContinuousは成功する：

GenerateConditions (2)

デフォルトで，FunctionContinuousは記号パラメータについての条件を生成することがある：

GenerateConditionsNoneのときは，FunctionContinuousは条件付きの結果を与えるのではなく失敗する：

以下は条件的に有効な結果を条件を述べずに返す：

デフォルトで，すべての条件が報告される：

GenerateConditionsAutomaticとすると，一般的に真である条件は報告されない：

PerformanceGoal (1)

PerformanceGoalを使って潜在的に高く付く計算を避ける：

デフォルト設定は使用可能なあらゆるテクニックを使って結果を出そうとする：

アプリケーション (14)

連続関数のクラス (6)

多項式は連続である：

Sin，Cos，Expは連続である：

これらの関数を可視化する：

これらの関数は，複素平面上でも連続である：

これらの関数を上で可視化する：

連続関数の逆数はであるところではどこでも連続である：

したがって，有理関数は実数上で連続であることもあれば連続でないこともある：

しかし，すべての非定数多項式が平面上に根を持つため，有理関数は上では決して連続ではない：

複素平面上で関数を可視化するとに爆発があるのが分かる：

CotとCscはSinとCosの有理関数なので，これらの関数は正弦が非零のところでは連続である：

これらの関数を正弦とともに可視化する：

同様に，TanとSecは余弦が非零のときは連続である：

これと同じ原理が双曲線三角関数のCothとCschにも当てはまる：

これらの関数をSinhとともに可視化する：

Coshは決して零にはならないので，残りの2つの関数のTanhとSechも連続である：

連続関数の複合関数は連続である：

非連続関数と連続関数の複合関数は，が定義域をの連続小領域に写像する限り連続である．例として，をSqrtとしよう．Sqrtは実数上で不連続である：

しかし，では連続である：

Expはに写像する：

したがって，SqrtとExpの合成関数は上で連続である：

多変量多項式は実数と複素数上で連続である：

多変量有理関数は実数上で連続のこともあれば連続ではないこともある：

複素数上では常に不連続である：

不連続有理関数が連続関数に拡張されることもある：

一変量連続関数と合成することで，より連続的な関数が生成される：

連続関数を可視化する：

微積分 (5)

連続関数の極限は代入によって計算される：

関数とは零以外の実線上で一致する：

Sincは連続である：

関数は連続ではない：

特に，原点で連続ではないので，その極限は代入では計算できない：

この2つの関数はについて等しいので，そこで同じ極限を持つ：

次の関数は不連続である：

これは原点でのみ不連続である：

この不連続点はがそこで定義されていないことによる：

しかし，はのとき極限を持つ：

をの原点までの拡張として定義する：

この拡張は連続関数である：

を可視化する：

関数は連続である：

しかし，第1導関数は連続ではない：

したがって，は解析的ではない：

は滑らかに零まで行くが，その導関数は原点で激しく振動する：

とその第1導関数を可視化する：

有界の関数の定積分は，たとえが不連続でも連続である．次のについて考える：

これは不連続である：

がその定積分の原点から任意の実数値までであると定義する：

関数は連続である：

この関数とその積分を可視化する：

確率 (3)

連続確率分布のCDFは連続である：

この関数を可視化する：

離散分布のCDFは不連続である：

これらの分布は区分定数累積分布関数を持つ：

混合分布のCDFは不連続である：

これらの分布は区分的ではあるが連続ではない累積分布関数を持つ：

特性と関係 (3)

連続関数の極限は定義域上の各点でその値と等しい：

Limitを使って極限を計算する：

ある区間内で連続な関数はその最小値と最大値の間の各値に達する：

MinimizeとMaximizeを使って最小値と最大値を求める：

が最小値と最大値の間にあることを確認する：

Solveを使ってが値に達する点を求める：

特性を図示する：

FunctionAnalyticを使って関数が解析的かどうかをチェックする：

解析的関数は連続である：

連続関数は解析的ではないことがある：

考えられる問題 (2)

関数が連続であるためにはあらゆるところで定義されなければならない：

関数が実領域で連続であるためには，その関数は実数値でなければならない：

トップへ