WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Tanh
✖
Tanh

✖
Tanh[z]

gives the hyperbolic tangent of z.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • Sinh[z]/Cosh[z] is automatically converted to Tanh[z]. TrigFactorList[expr] does decomposition.
  • For certain special arguments, Tanh automatically evaluates to exact values.
  • Tanh can be evaluated to arbitrary numerical precision.
  • Tanh automatically threads over lists. »
  • Tanh can be used with Interval and CenteredInterval objects. »

Background & Context

  • Tanh is the hyperbolic tangent function, which is the hyperbolic analogue of the Tan circular function used throughout trigonometry. Tanh[α] is defined as the ratio of the corresponding hyperbolic sine and hyperbolic cosine functions via 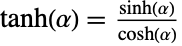. Tanh may also be defined as 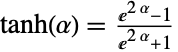, where 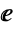is the base of the natural logarithm Log.
  • Tanh automatically evaluates to exact values when its argument is the (natural) logarithm of a rational number. When given exact numeric expressions as arguments, Tanh may be evaluated to arbitrary numeric precision. TrigFactorList can be used to factor expressions involving Tanh into terms containing Sinh, Cosh, Sin, and Cos. Other operations useful for manipulation of symbolic expressions involving Tanh include TrigToExp, TrigExpand, Simplify, and FullSimplify.
  • Tanh threads element-wise over lists and matrices. In contrast, MatrixFunction can be used to give the hyperbolic tangent of a square matrix (i.e. the power series for the hyperbolic tangent function with ordinary powers replaced by matrix powers) as opposed to the hyperbolic tangents of the individual matrix elements.
  • Tanh[x] approaches 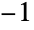for small negative x and 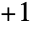for large positive x. Tanh satisfies an identity similar to the Pythagorean identity satisfied by Tan, namely 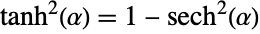. The definition of the hyperbolic tangent function is extended to complex arguments 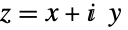by way of the identities 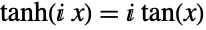and 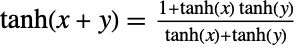. Tanh has poles at values 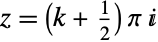for 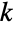an integer and evaluates to ComplexInfinity at these points. Tanh[z] has series expansion sum_(k=0)^infty(2^(2 k)(2^(2k)-1) TemplateBox[{{2, , k}}, BernoulliB] )/((2 k)!)z^(2 k-1) about the origin that may be expressed in terms of the Bernoulli numbers BernoulliB.
  • The inverse function of Tanh is ArcTanh. Additional related mathematical functions include Sinh, Coth, and Tan.

Examples

open allclose all

Basic Examples  (5)Summary of the most common use cases

Evaluate numerically:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-f8mh1d
Out[1]=1

Plot over a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ixm76y
Out[1]=1

Plot over a subset of the complexes:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-kiedlx
Out[1]=1

Series expansion at 0:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ewuwd9
Out[1]=1

Asymptotic expansion at a singular point:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-k12ao4
Out[1]=1

Scope  (46)Survey of the scope of standard use cases

Numerical Evaluation  (5)

Evaluate to high precision:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-29kz8
Out[1]=1

The precision of the output tracks the precision of the input:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-3ec16
Out[2]=2

Tanh can take complex number inputs:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ft1eky
Out[1]=1

Evaluate Tanh efficiently at high precision:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-bq2c6r
Out[2]=2

Compute the elementwise values of an array using automatic threading:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-thgd2
Out[1]=1

Or compute the matrix Tanh function using MatrixFunction:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-o5jpo
Out[2]=2

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-eacc3
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-lmyeh7
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-fr1lbp
Out[3]=3

Or compute average-case statistical intervals using Around:

In[4]:=4
✖
https://wolfram.com/xid/0y8aa9-cw18bq
Out[4]=4

Specific Values  (4)

Values of Tanh at fixed purely imaginary points:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-nww7l
Out[1]=1

Values at infinity:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-pmmsbf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-h2f1w1
Out[2]=2

Zero of Tanh:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-cw39qs
Out[1]=1

Find the zero using Solve:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-bgtr3o
Out[2]=2

Substitute in the value:

In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-oiazhe
Out[3]=3

Visualize the result:

In[4]:=4
✖
https://wolfram.com/xid/0y8aa9-lv6k6q
Out[4]=4

Simple exact values are generated automatically:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-c5kgx6
Out[1]=1

More complicated cases require explicit use of FunctionExpand:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-mnn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-p3j
Out[3]=3

Visualization  (3)

Plot the Tanh function:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ecj8m7
Out[1]=1

Plot the real part of :

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bo5grg
Out[1]=1

Plot the imaginary part of :

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-dx2pr
Out[2]=2

Plot the real part of :

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-epb4bn
Out[1]=1

Function Properties  (12)

Tanh is defined for all real values:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-cl7ele
Out[1]=1

Complex domain:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-de3irc
Out[2]=2

Tanh achieves all real values from the open interval :

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-evf2yr
Out[1]=1

Tanh is an odd function:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-dnla5q
Out[1]=1

Tanh has the mirror property tanh(TemplateBox[{z}, Conjugate])=TemplateBox[{{tanh, (, z, )}}, Conjugate]:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-heoddu
Out[1]=1

Tanh is an analytic function of over the reals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-h5x4l2
Out[1]=1

While it is not analytic on the complex plane, it is meromorphic:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-ez7tfw
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-4ddax2
Out[3]=3

Tanh is monotonic:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-g6kynf
Out[1]=1

Tanh is injective:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-gi38d7
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-ctca0g
Out[2]=2

Tanh is not surjective:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-hkqec4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-hdm869
Out[2]=2

Tanh is neither non-negative nor non-positive:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-84dui
Out[1]=1

Tanh has no singularities or discontinuities:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-mdtl3h
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-mn5jws
Out[2]=2

Tanh is neither convex nor concave:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-io426y
Out[1]=1

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-fh7jar

Differentiation  (3)

First derivative:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-mmas49
Out[1]=1

Higher derivatives:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-nfbe0l
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-5rzar
Out[2]=2

Formula for the ^(th) derivative:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-odmgl1
Out[1]=1

Integration  (3)

Indefinite integral of Tanh:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bponid
Out[1]=1

Definite integral of an odd integrand over an interval centered at the origin is 0:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-b9jw7l
Out[1]=1

More integrals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-c56p3v
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-k7rv16
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-g221sm
Out[3]=3

Series Expansions  (4)

Find the Taylor expansion using Series:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ewr1h8
Out[1]=1

Plot the first three approximations for Tanh around :

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-binhar
Out[2]=2

General term in the series expansion of Tanh:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ctla0e
Out[1]=1

A few first terms of Fourier series:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-f64drv
Out[1]=1

Tanh can be applied to power series:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-b8zc8w
Out[1]=1

Integral Transforms  (2)

Compute the Laplace transform using LaplaceTransform:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-ralmmn
Out[1]=1

FourierTransform:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-g4jpzm
Out[1]=1

Function Identities and Simplifications  (6)

Tanh of a double angle:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-mjplp7
Out[1]=1

Convert multiple‐angle expressions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-kvf23t
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-m77ks
Out[2]=2

Tanh of a sum:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-nfe4y
Out[1]=1

Convert sums of hyperbolic functions to products:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-nwd70
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-kcx5nz
Out[2]=2

Expand assuming real variables and :

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-jrl4k
Out[1]=1

Convert to exponentials:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-dvmv83
Out[1]=1

Function Representations  (4)

Representation through Tan:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-df304y
Out[1]=1

Representation through Bessel functions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-9y9s4
Out[1]=1

Representation through Jacobi functions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-cvvpzm
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-g9t7o2
Out[2]=2

Representation through Mathieu functions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-vmhy11
Out[1]=1

Applications  (4)Sample problems that can be solved with this function

Plot a tractrix pursuit curve:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-oj8qpy
Out[1]=1

Plot a pseudosphere:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-hzyvh9
Out[1]=1

Calculate the finite area of the surface extending to infinity:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-zzbr7
Out[2]=2

Velocity of a relativistic body in a constant force field:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bs2t69
Out[1]=1

Solution of the Burgers' equation using the tanh method:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bi3r23
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-j32fqt
Out[2]=2

Properties & Relations  (13)Properties of the function, and connections to other functions

Basic parity and periodicity properties of Tanh are automatically applied:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-kocj3w
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-ebh78
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-bqdwep
Out[3]=3

Expressions containing hyperbolic functions do not automatically simplify:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-jezq8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-g06vxs
Out[2]=2

Use Refine, Simplify, and FullSimplify to simplify expressions containing Tanh:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-lb9an5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-gff2zy
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-eb62d5
Out[3]=3

Use FunctionExpand to express special values in radicals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-b89r83
Out[1]=1

Compose with inverse functions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-fvbq9h
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-dbvt9m
Out[2]=2

Solve a hyperbolic equation:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-b6ntf8
Out[1]=1

Numerically find a root of a transcendental equation:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-skmzw
Out[1]=1

Reduce a hyperbolic equation:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bfl3o3
Out[1]=1

Integrals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-bw1qy5
Out[1]=1

Integral transforms:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-fmpx0y
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-drshlz
Out[2]=2

Obtain Tanh from sums and integrals:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-c5l23
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-bz0wge
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y8aa9-n3lbz0
Out[3]=3

Tanh appears in special cases of special functions:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-tuph9
Out[1]=1

Tanh is a numeric function:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-lqmofj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-bkvbk
Out[2]=2

Possible Issues  (4)Common pitfalls and unexpected behavior

Machine-precision input is insufficient to give a correct answer:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-iubygb
Out[1]=1

With exact input, the answer is correct:

In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-b5az2y
Out[2]=2

A larger setting for $MaxExtraPrecision can be needed:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-06gw2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-g33rc4
Out[2]=2

No power series exists at infinity, where Tanh has an essential singularity:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-cwihoi
Out[1]=1

In TraditionalForm, parentheses are needed around the argument:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-casrkv
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y8aa9-e7rnsl
Out[2]=2

Neat Examples  (1)Surprising or curious use cases

Continued fraction expansion:

In[1]:=1
✖
https://wolfram.com/xid/0y8aa9-b3bm5r
Out[1]=1
Wolfram Research (1988), Tanh, Wolfram Language function, https://reference.wolfram.com/language/ref/Tanh.html (updated 2021).
✖
Wolfram Research (1988), Tanh, Wolfram Language function, https://reference.wolfram.com/language/ref/Tanh.html (updated 2021).

Text

Wolfram Research (1988), Tanh, Wolfram Language function, https://reference.wolfram.com/language/ref/Tanh.html (updated 2021).

✖
Wolfram Research (1988), Tanh, Wolfram Language function, https://reference.wolfram.com/language/ref/Tanh.html (updated 2021).

CMS

Wolfram Language. 1988. "Tanh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Tanh.html.

✖
Wolfram Language. 1988. "Tanh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Tanh.html.

APA

Wolfram Language. (1988). Tanh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tanh.html

✖
Wolfram Language. (1988). Tanh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tanh.html

BibTeX

@misc{reference.wolfram_2025_tanh, author="Wolfram Research", title="{Tanh}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Tanh.html}", note=[Accessed: 22-May-2025 ]}

✖
@misc{reference.wolfram_2025_tanh, author="Wolfram Research", title="{Tanh}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Tanh.html}", note=[Accessed: 22-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_tanh, organization={Wolfram Research}, title={Tanh}, year={2021}, url={https://reference.wolfram.com/language/ref/Tanh.html}, note=[Accessed: 22-May-2025 ]}

✖
@online{reference.wolfram_2025_tanh, organization={Wolfram Research}, title={Tanh}, year={2021}, url={https://reference.wolfram.com/language/ref/Tanh.html}, note=[Accessed: 22-May-2025 ]}