Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

FunctionPoles

FunctionPoles[f,x]

finds the poles of the meromorphic function f with the variable x.

FunctionPoles[{f,cons},x]

gives the poles of f when x is restricted by the constraints cons.

Details and Options

Function poles are also known as pole singularities.
Function poles are often used to compute the residue of a function in complex analysis or to compute the radius of convergence for a power series.
A function 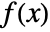has a pole singularity at 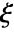with multiplicity 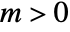if it has a series representation of the form 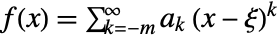. A function is meromorphic if it only has pole singularities.

FunctionPoles returns a list of pairs {pole,multiplicity}.
The function f should be meromorphic for x satisfying the constraints cons.
cons can contain equations, inequalities or logical combinations of these.
The following options can be given:

	Assumptions	$Assumptions	assumptions on parameters
	GeneratedParameters	C	how to name parameters that are generated
	PerformanceGoal	$PerformanceGoal	whether to prioritize speed or quality

Some of the returned poles may have Indeterminate multiplicity if FunctionPoles fails to determine their multiplicity.

Examples

open allclose all

Basic Examples (2)

Find poles of a rational function:

The set of poles may be infinite:

Scope (6)

A rational function:

A function with infinitely many poles:

Find the poles with :

Analytic functions have no poles:

has a removable singularity at :

FunctionPoles requires the input function to be meromorphic:

The function is meromorphic for :

Some of the returned poles may have Indeterminate multiplicity if determining the multiplicity fails:

Options (3)

Assumptions (1)

Specify conditions on parameters:

GeneratedParameters (1)

FunctionPoles may introduce new parameters to represent the solution:

Use GeneratedParameters to control how the parameters are named:

PerformanceGoal (1)

Computing multiplicities of poles may take a long time:

PerformanceGoal"Speed" limits the time allowed for computation of multiplicity:

The poles returned in both cases are the same:

In the first case, all multiplicities are computed successfully:

In the second case, some multiplicities are not computed:

Applications (3)

Classify singularities of a meromorphic function:

FunctionSingularities gives locations of poles and removable singularities:

has a double pole at , a single pole at and a removable singularity at :

Integrate $TemplateBox[{{{x, ^, 3}, -, {x, /, 3}}}, Gamma]$ along the unit circle:

Compute the poles of in the unit disk:

Compute the integral using the residue theorem:

Compare with the result of numeric integration:

Find the radius of convergence of the Taylor series of at :

The radius of convergence equals the distance to the nearest pole:

Even though the poles are complex, the convergence over the reals is affected:

Since is farther from the poles than , the convergence radius at is greater:

Properties & Relations (4)

The limit of the absolute value of a function at a pole is :

Use Limit to compute the limit:

The first term of the power series of a function at a pole of multiplicity has exponent :

Use Series to compute the series:

Use Residue to find the coefficient at the series term with exponent :

The only singularities a meromorphic function can have are poles and removable singularities:

Use FunctionSingularities to find a condition satisfied by all singularities:

Use SolveValues to find the singularities:

The function has poles at and and a removable singularity at :

Use FunctionPoles to find the poles of a function:

Use Residue to find the residues at the poles:

ResidueSum gives the sum of the residues at all poles:

Possible Issues (2)

Some of the returned poles may have Indeterminate multiplicity if determining the multiplicity fails:

FunctionPoles rationalizes inexact inputs and then approximates the result to the input precision:

The result may depend on which rational numbers are chosen:

In the first example, the rationalized exponent is an integer; in the second example, it is not:

Top