FunctionSingularities
x∈Reals,求 ![]() 的奇点.
的奇点.
FunctionSingularities[f,x,dom]
x∈dom,求 ![]() 的奇点.
的奇点.
FunctionSingularities[{f1,f2,…},{x1,x2,…},dom]
x1,x2,…∈dom,求 ![]() 的奇点.
的奇点.
更多信息


- 函数的奇点通常用于查找保证函数解析的区域或查找需要进行特殊分析的点和曲线.
- FunctionSingularities 给出使得
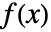 在
在 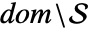 中解析的集合
中解析的集合 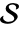 的隐式描述. 不能保证集合
的隐式描述. 不能保证集合 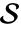 是最小的.
是最小的. - 所得的隐式描述由等式、不等式、域的规范以及它们的逻辑组合组成,适合用在 Reduce 和 Solve 等函数中.
- 奇点有多种来源,包括 Laurent 级数表示、多值函数以及函数的分段和部分定义.
- 来自 Laurent 级数表示
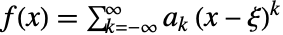 的奇点,其中
的奇点,其中 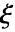 是孤立奇点的位置:
是孤立奇点的位置: -
可移除奇点 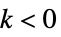 时,
时,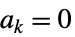 ,比如:
,比如: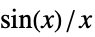 ,当
,当 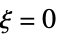 时
时极点 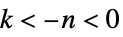 时,
时,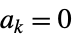 ,比如:
,比如: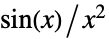 ,当
,当 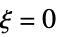 时
时本性奇点 对于无穷多的 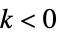 ,
,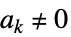 ,比如:
,比如: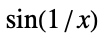 ,当
,当 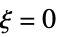 时
时非本性奇点 极点或可移除奇点 - 来自多值函数的主要分支的选择的奇点:
-
分支点 多值函数的分支汇合的点,如 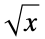 ,当
,当 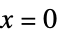 时
时分支切割 函数在其上不连续以获得单值函数的曲线,如 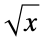 ,当
,当 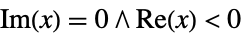 时
时 - 来自分段定义的函数或自然定义域的奇点:
-
分段函数 分段定义的函数,如 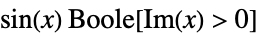 ,当
,当 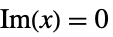 时
时定义域 定义域的补集,如 ![TemplateBox[{1, {1, /, 2}, x}, EllipticTheta] TemplateBox[{1, {1, /, 2}, x}, EllipticTheta]](Files/FunctionSingularities.zh/28.png) ,当
,当 ![TemplateBox[{x}, Abs]>=1 TemplateBox[{x}, Abs]>=1](Files/FunctionSingularities.zh/29.png) 时
时 - 对于多变量函数,奇点为每个变量的奇点.
- dom 的可能的值为 Reals 和 Complexes.
范例
打开所有单元关闭所有单元范围 (5)
应用 (6)
属性和关系 (3)
在 FunctionSingularities 给出的集合外函数是解析的:
用 FunctionAnalytic 查看解析性:
FunctionDiscontinuities 给出一个集合,函数在该集合外连续:
FunctionSingularities 求所有奇点都满足的条件:
使用 SolveValues 求得奇点:
使用 FunctionPoles 求得极点奇异性及其多重性:
Wolfram Research (2020),FunctionSingularities,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FunctionSingularities.html.
文本
Wolfram Research (2020),FunctionSingularities,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FunctionSingularities.html.
CMS
Wolfram 语言. 2020. "FunctionSingularities." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSingularities.html.
APA
Wolfram 语言. (2020). FunctionSingularities. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FunctionSingularities.html 年