FunctionSurjective[f,x]
tests whether ![]() has at least one solution
has at least one solution ![]() for each y∈Reals.
for each y∈Reals.
FunctionSurjective[f,x,dom]
tests whether ![]() has at least one solution x∈dom for each y∈dom.
has at least one solution x∈dom for each y∈dom.
FunctionSurjective[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() has at least one solution x1,x2,…∈dom for each y1,y2,…∈dom.
has at least one solution x1,x2,…∈dom for each y1,y2,…∈dom.
FunctionSurjective[{funs,xcons,ycons},xvars,yvars,dom]
tests whether ![]() has at least one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
has at least one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.


FunctionSurjective
FunctionSurjective[f,x]
tests whether ![]() has at least one solution
has at least one solution ![]() for each y∈Reals.
for each y∈Reals.
FunctionSurjective[f,x,dom]
tests whether ![]() has at least one solution x∈dom for each y∈dom.
has at least one solution x∈dom for each y∈dom.
FunctionSurjective[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() has at least one solution x1,x2,…∈dom for each y1,y2,…∈dom.
has at least one solution x1,x2,…∈dom for each y1,y2,…∈dom.
FunctionSurjective[{funs,xcons,ycons},xvars,yvars,dom]
tests whether ![]() has at least one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
has at least one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
Details and Options

- A surjective function is also known as onto or an onto mapping.
- A function
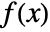 is surjective if for every
is surjective if for every 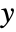 there is at least one
there is at least one 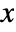 such that
such that 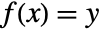 .
. - If funs contains parameters other than xvars, the result is typically a ConditionalExpression.
- Possible values for dom are Reals and Complexes. If dom is Reals, then all variables, parameters, constants and function values are restricted to be real.
- The domain of funs is restricted by the condition given by FunctionDomain.
- xcons and ycons can contain equations, inequalities or logical combinations of these.
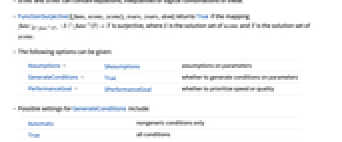
- FunctionSurjective[{funs,xcons,ycons},xvars,yvars,dom] returns True if the mapping
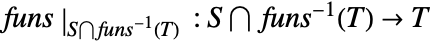 is surjective, where
is surjective, where 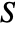 is the solution set of xcons and
is the solution set of xcons and 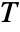 is the solution set of ycons.
is the solution set of ycons. - The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions True whether to generate conditions on parameters PerformanceGoal $PerformanceGoal whether to prioritize speed or quality - Possible settings for GenerateConditions include:
-
Automatic nongeneric conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal are "Speed" and "Quality".
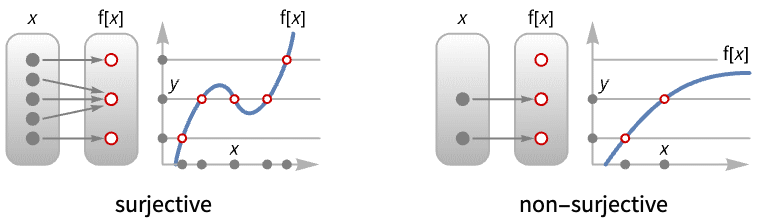
Examples
open all close allBasic Examples (4)
Scope (12)
Each value is attained at least once:
Surjectivity over a subset of the reals:
For positive ![]() , some values are not attained:
, some values are not attained:
Surjectivity onto a subset of the reals:
Each positive value ![]() is for some positive
is for some positive ![]() :
:
Surjectivity over the complexes:
The value zero is not attained:
Surjectivity onto a subset of complexes:
Surjectivity over the integers:
Surjectivity of linear mappings:
A linear mapping is surjective iff the rank of its matrix is equal to the dimension of its codomain:
Surjectivity of polynomial mappings ![]() :
:
Each value is attained at least once:
This mapping is not surjective:
Surjectivity of polynomial mappings ![]() :
:
Surjectivity of polynomial mappings ![]() :
:
Surjectivity of a real polynomial with symbolic parameters:
Surjectivity of a real polynomial mapping with symbolic parameters:
Options (4)
Assumptions (1)
FunctionSurjective gives a conditional answer here:
This checks the surjectivity for the remaining real values of ![]() :
:
GenerateConditions (2)
By default, FunctionSurjective may generate conditions on symbolic parameters:
With GenerateConditionsNone, FunctionSurjective fails instead of giving a conditional result:
This returns a conditionally valid result without stating the condition:
By default, all conditions are reported:
With GenerateConditionsAutomatic, conditions that are generically true are not reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
Applications (11)
Basic Applications (7)
![]() is surjective because it attains each value at least once:
is surjective because it attains each value at least once:
![]() is not surjective because the value
is not surjective because the value ![]() is not attained:
is not attained:
![]() is not surjective because it does not attain negative values:
is not surjective because it does not attain negative values:
![]() is surjective as a function from
is surjective as a function from ![]() to
to ![]() :
:
Each non-negative value is attained:
Each value is attained at least once:
Some values, e.g. ![]() , are not attained:
, are not attained:
A function is surjective if any horizontal line intersects its graph at least once:
If a horizontal line does not intersect the graph, the function is not surjective:
Bounded functions are not surjective:
If ![]() is continuous on
is continuous on ![]() and
and ![]() , then
, then ![]() is surjective onto
is surjective onto ![]() :
:
Use FunctionContinuous to check that ![]() is continuous in
is continuous in ![]() :
:
By the intermediate value theorem, ![]() restricted to
restricted to ![]() is surjective onto
is surjective onto ![]() :
:
An affine mapping ![]() is surjective if the rank of
is surjective if the rank of ![]() is equal to the number of rows of
is equal to the number of rows of ![]() :
:
Solving Equations and Inequalities (1)
A function ![]() is surjective if the equation
is surjective if the equation ![]() has at least one solution for any
has at least one solution for any ![]() :
:
For each real ![]() , there is at least one real solution for
, there is at least one real solution for ![]() :
:
Use Resolve to check the condition expressed using quantifiers:
Probability & Statistics (3)
A CDF for a continuous distribution is surjective onto the interval of probabilities (0,1) over its domain:
A SurvivalFunction for a continuous distribution is surjective onto the interval of probabilities (0,1) over its domain:
The quantile function Quantile for a distribution is surjective onto the domain of the distribution:
Properties & Relations (3)
![]() is surjective iff the equation
is surjective iff the equation ![]() has at least one solution for each
has at least one solution for each ![]() :
:
Use Solve to find the solutions:
A real continuous function on an interval is surjective iff the limits at endpoints are ![]() and
and ![]() :
:
Use Limit to compute the limits:
A function is surjective if its FunctionRange is True:
Possible Issues (1)
FunctionSurjective determines the real domain of functions using FunctionDomain:
![]() is not surjective onto
is not surjective onto ![]() in the real domain reported by FunctionDomain:
in the real domain reported by FunctionDomain:
![]() is real valued over the whole reals and is surjective onto
is real valued over the whole reals and is surjective onto ![]() :
:
All subexpressions of ![]() need to be real valued for a point to belong to the real domain of
need to be real valued for a point to belong to the real domain of ![]() :
:
Related Guides
History
Text
Wolfram Research (2020), FunctionSurjective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSurjective.html.
CMS
Wolfram Language. 2020. "FunctionSurjective." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSurjective.html.
APA
Wolfram Language. (2020). FunctionSurjective. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSurjective.html
BibTeX
@misc{reference.wolfram_2025_functionsurjective, author="Wolfram Research", title="{FunctionSurjective}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSurjective.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionsurjective, organization={Wolfram Research}, title={FunctionSurjective}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSurjective.html}, note=[Accessed: 14-February-2026]}