是 Graph 和相关函数的一个选项,指定使用哪种布局.


GraphLayout
布局方式列表 »是 Graph 和相关函数的一个选项,指定使用哪种布局.
更多信息





- 通常使用几个阶段计算图布局. 设置 GraphLayout->{s1->m1,…} 下,阶段 si 由方法 mi 处理.
- 可能的图布局阶段 si 是:
-
"VertexLayout" 如何嵌入顶点 "EdgeLayout" 如何规划边 "PackingLayout" 如何放置顶点组成的连通分量 - "VertexLayout" 方法包括:
-
Automatic 自动选择布局 None 不计算布局 "emb" 已命名的嵌入 - 可能的特殊嵌入 "emb" 包括:
-

"BipartiteEmbedding" 两条平行线上的顶点 
"CircularEmbedding" 圆圈上的顶点 
"CircularMultipartiteEmbedding" 圆圈弧段上的顶点 
"DiscreteSpiralEmbedding" 离散螺旋上的顶点 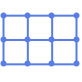
"GridEmbedding" 网格上的顶点 
"LinearEmbedding" 直线上的顶点 
"MultipartiteEmbedding" 几条平行线上的顶点 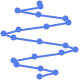
"SpiralEmbedding" 投射到二维的三维螺旋上的顶点 
"StarEmbedding" 带中心点的圆圈上的顶点 - 对于诸如树和有向无环图这样的分层图,可能的结构化嵌入 "emb" 包括:
-

"BalloonEmbedding" 以父顶点为中心的圆圈上的顶点 
"RadialEmbedding" 圆形弧段上的顶点 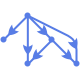
"LayeredDigraphEmbedding" 有向无环图平行线上的顶点 
"LayeredEmbedding" 平行线上的顶点 
"SymmetricLayeredEmbedding" 对称平行线上的顶点 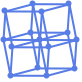
"HyperbolicRadialEmbedding" 庞加莱圆盘上圆弧的顶点 - 可能的最优化嵌入 "emb" 都会最小化一个数量,包括:
-
"GravityEmbedding" 顶点为质点,边为弹簧的能量 
"HighDimensionalEmbedding" 高维空间中的弹簧-电子能量 
"PlanarEmbedding" 边交叉数目 
"SpectralEmbedding" 平方距离的加权和 
"SphericalEmbedding" 顶点在球面上且边作为弹簧的能量 
"SpringElectricalEmbedding" 以边为弹簧,以顶点为电子的能量 
"SpringEmbedding" 以边为弹簧的能量 
"TutteEmbedding" 边的交叉数目和到邻居的距离 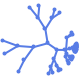
"HyperbolicSpringEmbedding" 庞加莱圆盘上以边为弹簧的能量 - "EdgeLayout" 方法包括:
-
"DividedEdgeBundling" 把边划分为线段束 "HierarchicalEdgeBundling" 根据分层树结构划分边 "StraightLine" 边之间的直线 - "PackingLayout" 方法包括:
-
"ClosestPacking" 从左上方开始的近似最紧密封装 "ClosestPackingCenter" 从中心开始的近似最紧密封装 "Layered" 从左上方开始按照层次排列 "LayeredLeft" 从左边开始按照层次排列 "LayeredTop" 从顶部开始按照层次排列 "NestedGrid" 在一个嵌套网格上排列
范例
打开所有单元 关闭所有单元范围 (131)
基本用途 (3)
顶点布局 (116)
"BalloonEmbedding" (8)
"BalloonEmbedding" 对树图效果最好:
使用选项 "EvenAngle"->True 把顶点均匀放在闭合圆圈内:
设置 "OptimalOrder"->True 下,顶点排序优化了角度和高宽比:
"BipartiteEmbedding" (2)
"CircularEmbedding" (4)
"CircularEmbedding" 最适合于循环图、LCF 符号嵌入和圈图:
"CircularMultipartiteEmbedding" (3)
"CircularMultipartiteEmbedding" 最适合于 k-分图:
"DiscreteSpiralEmbedding" (3)
"GravityEmbedding" (2)
"HighDimensionalEmbedding" (3)
"HyperbolicRadialEmbedding" (4)
"HyperbolicSpringEmbedding" (10)
"HyperbolicSpringEmbedding" 最适合树状图:
采用设置 "EdgeWeighted"True 时,将使用边的权重:
用选项 "EnergyControl"e 在最小化过程中指定系统总能量的限制:
用 "InferentialDistance"d 指定一个截止距离,超过该距离则假定顶点间的相互作用不存在:
用 "MaxIteration"it 来指定在尝试最小化能量时所采用的最大迭代次数:
用 "RandomSeed"int 为计算初始顶点布局的随机数生成器指定种子:
用 "StepControl"method 来定义怎样在能量最小化过程中调整步长:
"LayeredEmbedding" (7)
"LayeredEmbedding" 对树图效果最好:
使用选项 "LayerSizeFunction"->func 指定相对高度:
使用选项 "LeafDistance"->d 指定叶子距离:
"LayeredDigraphEmbedding" (7)
"LayeredDigraphEmbedding" 对有向无环图效果最好:
使用选项 "Orientation"->o 绘制具有不同方向的树:
"LinearEmbedding" (2)
"MultipartiteEmbedding" (3)
"PlanarEmbedding" (2)
"RadialEmbedding" (5)
"RadialEmbedding" 对树图效果最好:
"SpectralEmbedding" (3)
"SphericalEmbedding" (2)
"SpiralEmbedding" (3)
"SpringElectricalEmbedding" (15)
放置顶点,使得当每个顶点对应一个电子而每条边对应一条弹簧时,最小化它们的机械和电子能量:
"SpringElectricalEmbedding" 对大多数图效果都最好:
设置 "EdgeWeighted"->True 下,使用边权值:
使用选项 "EnergyControl"->e 指定在最小化过程中系统总能量的限制:
使用 "InferentialDistance"->d 指定假设顶点之间不存在交互作用的截止距离:
使用 "MaxIteration"->it 指定在尝试最小化能量的过程中所使用的最大迭代次数:
使用 "Multilevel"->method 指定在图的粗化的递归过程中所使用的方法:
设置 "Octree"->True 下,使用八叉树的数据结构(三维情形)或四叉树的数据结构(二维情形)计算排斥力:
使用 "RandomSeed"->int 指定计算初始顶点位置的随机数生成器的种子:
使用 "RepulsiveForcePower"->r 控制斥力随着距离衰减的有多快:
使用 "StepControl"->method 定义在能量最小化过程中如何修改步长:
"SpringEmbedding" (12)
放置顶点,以使得当每个边对应于一个弹簧时,最小化它们的机械能量:
"SpringEmbedding" 对规则结构化图效果最好:
设置 "EdgeWeighted"->True 下,使用边权值:
使用选项 "EnergyControl"->e 指定在最小化过程中系统总能量的限制:
使用 "InferentialDistance"->d 指定假定顶点之间不存在交互作用的截止距离:
使用 "MaxIteration"->it 指定在尝试最小化能量的过程中使用的最大迭代次数:
使用 "Multilevel"->method 指定在图的粗化递归过程中使用的方法:
使用 "RandomSeed"->int 指定计算初始顶点位置的随机数生成器的种子:
使用 "StepControl"->method 顶点在能量最小化过程中如何修改步长:
"StarEmbedding" (4)
"SymmetricLayeredEmbedding" (4)
"TutteEmbedding" (2)
边的布局 (3)
封装布局 (6)
属性和关系 (6)
GraphLayout 可用于普通图:
VertexCoordinates 会覆盖 GraphLayout 坐标:
利用 AbsoluteOptions 来提取通过布局算法计算所得的 VertexCoordinates:
相关指南
-
▪
- 图的样式、标记和布局 ▪
- 图的可视化 ▪
- 图的属性 ▪
- 图注解 ▪
- 图与网络
文本
Wolfram Research (2010),GraphLayout,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GraphLayout.html (更新于 2025 年).
CMS
Wolfram 语言. 2010. "GraphLayout." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/GraphLayout.html.
APA
Wolfram 语言. (2010). GraphLayout. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphLayout.html 年
BibTeX
@misc{reference.wolfram_2025_graphlayout, author="Wolfram Research", title="{GraphLayout}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GraphLayout.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphlayout, organization={Wolfram Research}, title={GraphLayout}, year={2025}, url={https://reference.wolfram.com/language/ref/GraphLayout.html}, note=[Accessed: 12-March-2026]}