GraphProduct

GraphProduct[g1,g2]

gives the Cartesian product of the graphs g1 and g2.

GraphProduct[g1,g2,"op"]

gives the product of type "op" for the graphs g1 and g2

Details and Options

  • GraphProduct is also known as box product.
  • GraphProduct is typically used to produce new graphs from Boolean combinations of initial graphs.
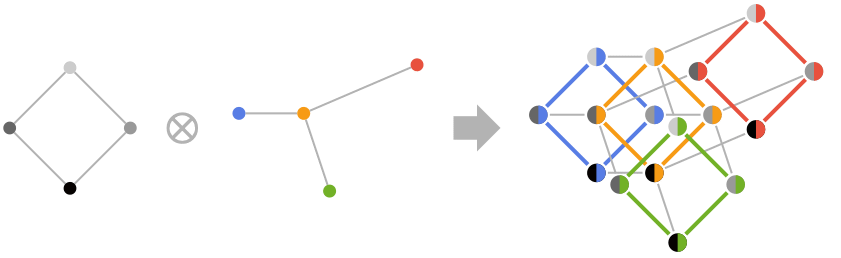
  • GraphProduct[g1,g2] gives a graph with vertices formed from the Cartesian product of the vertices of g1 and vertices of g2. The vertices {u1,u2} and {v1,v2} are connected if u1v1 and u2 is connected to v2, or u2v2 and u1 is connected to v1.
  • GraphProduct[g1,g2,"op"] gives a graph product of type "op" with edges {u1,u2}{v1,v2} subject to the following conditions:
  • "Cartesian"(u1v1 ∧ u2v2)∨(u2v2∧u1v1)
    "Conormal"(u1v1)∨(u2v2)
    "Lexicographical"(u1v1)∨(u1v1∧u2v2)
    "Normal"(u1v1∧u2v2)∨(u2v2∧u1v1)∨(u1v1∧u2v2)
    "Rooted"(u1v1 ∧ u2v2)∨(u1v1 ∧ u2v2r)
    "Tensor"(u1v1)∧(u2v2)
  • The vertex r is the first vertex in VertexList[g2].
  • GraphProduct[g1,g2] is effectively equivalent to GraphProduct[g1,g2,"Cartesian"].
  • GraphProduct works with undirected graphs, directed graphs, multigraphs and mixed graphs.

Examples

open allclose all

Basic Examples  (3)

Cartesian product of two graphs:

A table of graph products:

Generate grid graphs:

Torus graphs:

Scope  (30)

Directed Graphs  (5)

GraphProduct works with directed graphs:

Simple directed graphs:

Directed multigraphs:

Directed weighted graphs:

Directed annotated graphs:

Undirected Graphs  (5)

GraphProduct works with undirected graphs:

Simple undirected graphs:

Undirected multigraphs:

Undirected weighted graphs:

Undirected annotated graphs:

Mixed Graphs  (5)

GraphProduct works with mixed graphs:

Simple mixed graphs:

Mixed multigraphs:

Mixed weighted graphs:

Mixed annotated graphs:

Multigraphs  (5)

GraphProduct works with multigraphs:

Directed multigraphs:

Mixed multigraphs:

Weighted multigraphs:

Annotated multigraphs:

Weighted Graphs  (5)

GraphProduct works with weighted graphs:

Directed weighted graphs:

Undirected weighted graphs:

Mixed weighted graphs:

Annotated weighted graphs:

Special Graphs  (5)

GraphProduct works on entity graphs:

GraphProduct works on trees:

Use rules to specify the graph:

GraphProduct works with more than two graphs:

Generate a list of different graph products:

Properties & Relations  (6)

For two graphs with vi vertices, the number of vertices of their product is v1 v2 :

For two undirected graphs with vi vertices and ei edges, the number of edges of the Cartesian product is v1 e2+v2 e1:

Tensor product is 2 e1e2:

Lexicographical product is v1 e2+ e1v22 :

Normal product is v1 e2+v2 e1 + 2 e1e2:

Co-normal product is v12 e2+ e1v22 - 2e1e2:

Rooted product is v1 e2+ e1:

The Cartesian product of two single edges is a cycle:

The normal product of two single edges is a complete graph:

The tensor product of two single edges is a cross:

TorusGraph[{m,n}] is the graph formed from the Cartesian product of the cycle graphs and :

Wolfram Research (2022), GraphProduct, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphProduct.html.

Text

Wolfram Research (2022), GraphProduct, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphProduct.html.

CMS

Wolfram Language. 2022. "GraphProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GraphProduct.html.

APA

Wolfram Language. (2022). GraphProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphProduct.html

BibTeX

@misc{reference.wolfram_2025_graphproduct, author="Wolfram Research", title="{GraphProduct}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/GraphProduct.html}", note=[Accessed: 30-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_graphproduct, organization={Wolfram Research}, title={GraphProduct}, year={2022}, url={https://reference.wolfram.com/language/ref/GraphProduct.html}, note=[Accessed: 30-July-2025 ]}