GraphProduct
GraphProduct[g1,g2]
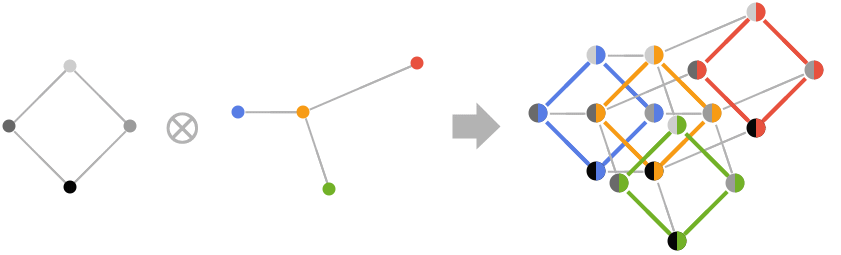
给出图 g1 和 g2 的笛卡尔积.
GraphProduct[g1,g2,"op"]
给出图 g1 和 g2 的 "op" 类型的积.
更多信息和选项

- GraphProduct 亦称为框积.
- GraphProduct 通常用于从初始图的布尔组合生成新图.
- GraphProduct[g1,g2] 给出一个图,其顶点由 g1 的顶点和 g2 的顶点的笛卡尔积形成. 如果 u1==v1 且 u2 与 v2 相连,或 u2==v2 且 u1 与 v1 相连,则顶点 {u1,u2} 和 {v1,v2} 相连.
- GraphProduct[g1,g2,"op"] 给出类型为 "op" 的图的积,其中的边 {u1,u2}{v1,v2} 受以下条件限制:
-
"Cartesian" (u1==v1 ∧ u2v2)∨(u2==v2∧u1v1) "Conormal" (u1v1)∨(u2v2) "Lexicographical" (u1v1)∨(u1==v1∧u2v2) "Normal" (u1==v1∧u2v2)∨(u2==v2∧u1v1)∨(u1v1∧u2v2) "Rooted" (u1==v1 ∧ u2v2)∨(u1v1 ∧ u2==v2==r) "Tensor" (u1v1)∧(u2v2) - 顶点 r 为 VertexList[g2] 中的第一个顶点.
- GraphProduct[g1,g2] 实际上等价于 GraphProduct[g1,g2,"Cartesian"].
- GraphProduct 适用于无向图、有向图、多重图和混合图.
范例
打开所有单元关闭所有单元范围 (30)
有向图 (5)
无向图 (5)
混合图 (5)
多重图 (5)
加权图 (5)
特殊的图 (5)
属性和关系 (6)
对于顶点为 vi 的两个图,它们的积的顶点的数量为 v1 v2 :
对于顶点为 vi、边为 ei 的两个无向图,它们的笛卡尔积的边的数量为 v1 e2+v2 e1:
TorusGraph[{m,n}] 是循环图 ![]() 和
和 ![]() 的笛卡尔积形成的图:
的笛卡尔积形成的图:
Wolfram Research (2022),GraphProduct,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GraphProduct.html.
文本
Wolfram Research (2022),GraphProduct,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GraphProduct.html.
CMS
Wolfram 语言. 2022. "GraphProduct." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GraphProduct.html.
APA
Wolfram 语言. (2022). GraphProduct. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphProduct.html 年