HadamardMatrix

HadamardMatrix[n]

n×n Hadamard行列を返す．

詳細とオプション

  • Hadamard行列の各項 Hrsは，デフォルトで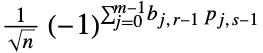，と定義される．ただし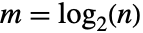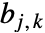，，は整数 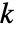のバイナリ表現における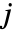 番目のビット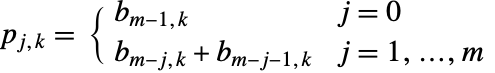， である．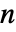
  • は2の累乗でなければならない．
  • HadamardMatrixの行または列はDiscreteHadamardTransformの基底数列である．
  • Hadamard行列は対称かつ直交で，それ自身の逆行列である． »
  • サポートされるオプション
  • Method Automatic数列順序メソッドを指定
    WorkingPrecision ∞行列要素の計算に使う精度
  • Methodオプションの設定は，連続順序（Hadamard基底数列内のゼロ交差数）を指定する．次は，可能な設定である．
  • "BitComplement"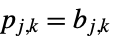
    "GrayCode""BitComplement"のGrayコード順序
    "Sequency"行と列の添字によって連続性が増す（デフォルト）
  • ビット補数順序はSylvester順序としても知られている．
  • 連続順序はWalsh順序としても知られている．
  • Grayコード順序は，二項順序またはPaley順序としても知られている．
  • HadamardMatrix[…,TargetStructure…]は返す行列の構造を指定する．次は， TargetStructureの可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Hermitian"行列をエルミート行列として表す
    "Orthogonal"行列を直交行列として表す
    "Symmetric"行列を対称行列として表す
    "Unitary"行列をユニタリ行列として表す
  • HadamardMatrix[…,TargetStructureAutomatic]はHadamardMatrix[…,TargetStructure"Dense"]に等しい．

例題

すべて開くすべて閉じる

例  (1)

Hadamard行列：

Hadamardの長さ128の基底数列：

オプション  (3)

Method  (1)

Hadamard行列の行のシーケンシーの値を検出する：

TargetStructure  (1)

Hadamard行列を密な行列として返す：

Hadamard行列を対称行列として返す：

Hadamard行列を直交行列として返す：

WorkingPrecision  (1)

デフォルトで，厳密行列が計算される：

機械精度を使う：

任意精度を使う：

特性と関係  (4)

ベクトルの離散Hadamard変換はベクトルにHadamard行列を掛けることに等しい：

階数4のSylvester型Hadamard行列：

これは，ビット補数連続順序に対応する：

Hadamard行列は対称かつ直交である：

この特性のため，アダマール行列はそれ自身の逆行列である：

n×n「ビット逆転」置換行列を定義する，ただし，n は2の累乗である：

n×n Gray コード置換行列を定義する．ただし，n は2の累乗である：

異なる連続順序でHadamard行列を生成する：

Grayコード順序のHadamard行列は，Grayコード置換をビット補数連続順序のHadamard行列に適用したものに等しい：

連続順序のHadamard行列は，ビット逆転置換をGrayコード順序のHadamard行列に適用したものに等しい：

連続順序のHadamard行列は，ビット逆転置換とGrayコード置換をビット補数連続順序Hadamard行列に連続的に適用したものに等しい：

Wolfram Research (2012), HadamardMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/HadamardMatrix.html （2024年に更新）.

テキスト

Wolfram Research (2012), HadamardMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/HadamardMatrix.html （2024年に更新）.

CMS

Wolfram Language. 2012. "HadamardMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/HadamardMatrix.html.

APA

Wolfram Language. (2012). HadamardMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HadamardMatrix.html

BibTeX

@misc{reference.wolfram_2024_hadamardmatrix, author="Wolfram Research", title="{HadamardMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HadamardMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hadamardmatrix, organization={Wolfram Research}, title={HadamardMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HadamardMatrix.html}, note=[Accessed: 22-November-2024 ]}