HarmonicMean
HarmonicMean[data]
gives the harmonic mean of the values in data.
Details
- For VectorQ data
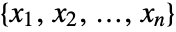, the harmonic mean is given by 
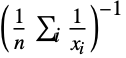. - For MatrixQ data, HarmonicMean[{{x1,y1},{x2,y2},…}] is equivalent to {HarmonicMean[{x1,x2,…}],HarmonicMean[{y1,y2,…}]}. »
- HarmonicMean handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData weighted mean, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels »
Examples
open allclose allScope (12)
Basic Uses (6)
Exact input yields exact output:
Approximate input yields approximate output:
Find the harmonic mean of WeightedData:
Find the harmonic mean of EventData:
Find the harmonic mean of a TimeSeries:
The harmonic mean depends only on the values:
Array Data (4)
HarmonicMean for a 2D matrix gives columnwise means:
SparseArray data can be used just like dense arrays:
Find the harmonic mean of a QuantityArray:
Image and Audio Data (2)
Channelwise harmonic mean value of an RGB image:
Harmonic mean intensity value of a grayscale image:
On audio objects, HarmonicMean works channelwise:
Properties & Relations (6)
HarmonicMean is the inverse of Mean of the inverse of the data:
HarmonicMean is very sensible to values close to zero:
This agrees with the definition:
HarmonicMean is logarithmically related to GeometricMean for positive values:
For positive data 
, HarmonicMean[d]≤GeometricMean[d]≤Mean[d]:
Prove the inequality symbolically:
HarmonicMean[Range[n]] is inversely related to HarmonicNumber[n]:
The harmonic mean of the shifted data is larger than the shifted harmonic mean of the original data (assuming the shift is a positive number):
Possible Issues (1)
HarmonicMean will return 0 when the audio channels have a 0 in them; this is common for real-world audio samples:
Mean will clip channel values to values that can be represented with machine numbers:
Text
Wolfram Research (2007), HarmonicMean, Wolfram Language function, https://reference.wolfram.com/language/ref/HarmonicMean.html (updated 2023).
CMS
Wolfram Language. 2007. "HarmonicMean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/HarmonicMean.html.
APA
Wolfram Language. (2007). HarmonicMean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HarmonicMean.html